《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

5. 如图28 - 2 - 8所示，在△ABC中，∠A = 45°，AC = $\sqrt{2}$，AB = $\sqrt{3}+1$，则边BC的长为 _______.

答案： 2@@解析：过点 C 作 $CD\perp AB$ 于点 D，在 $Rt\triangle ACD$ 中，∠A = 45°，
∴ $AD = CD = AC\cdot\sin A = 1$，
∴ $BD=\sqrt{3}+1 - 1=\sqrt{3}$。 在 $Rt\triangle BCD$ 中，由勾股定理得 $BC=\sqrt{CD^{2}+BD^{2}}=\sqrt{1^{2}+(\sqrt{3})^{2}} = 2$。

6. 如图28 - 2 - 9所示，在Rt△ABC中，∠C = 90°，AB = 10，sin A = $\frac{2}{5}$，求BC的长和tan B的值.

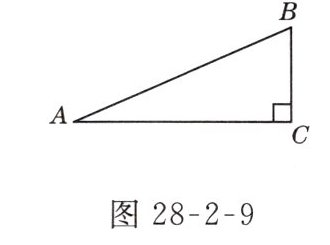
答案： 解：
∵ $\sin A=\frac{BC}{AB}=\frac{2}{5}$，$AB = 10$，
∴ $BC = 4$。 又 $AC=\sqrt{AB^{2}-BC^{2}} = 2\sqrt{21}$，
∴ $\tan B=\frac{AC}{BC}=\frac{\sqrt{21}}{2}$。

一、选择题
1. 在Rt△ACB中，∠C = 90°，AB = 10，sin A = $\frac{3}{5}$，cos A = $\frac{4}{5}$，tan A = $\frac{3}{4}$，则BC的长为（ ）
A. 6
B. 7.5
C. 8
D. 12.5

答案： A@@解析：由 $\sin A=\frac{BC}{AB}$，得 $BC = AB\cdot\sin A = 10\times\frac{3}{5}=6$。

2. 如图28 - 2 - 10所示，在矩形ABCD中，DE⊥AC于点E，设∠ADE = α，且cos α = $\frac{3}{5}$，AB = 4，则AD的长为（ ）

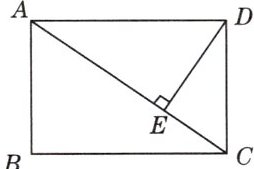
A. 3
B. $\frac{16}{3}$
C. $\frac{20}{3}$
D. $\frac{16}{5}$

答案： B@@解析：
∵ $DE\perp AC$，
∴ ∠DAE + ∠ADE = 90°。 又 ∠DAE + ∠BAC = 90°，
∴ ∠ADE = ∠BAC = α。
∴ $\cos\alpha=\cos\angle BAC=\frac{AB}{AC}=\frac{3}{5}$。 又 $AB = 4$，
∴ $AC=\frac{20}{3}$，
∴ $AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{(\frac{20}{3})^{2}-4^{2}}=\frac{16}{3}$。

二、填空题
3. 在Rt△ABC中，∠C = 90°，b = 3，c = 2$\sqrt{3}$，则a = _______，∠A = _______.

答案： $\sqrt{3}$@@30°@@解析：$a=\sqrt{c^{2}-b^{2}}=\sqrt{(2\sqrt{3})^{2}-3^{2}}=\sqrt{3}$。
∵ $\sin A=\frac{a}{c}=\frac{\sqrt{3}}{2\sqrt{3}}=\frac{1}{2}$，
∴ ∠A = 30°。

4. 在Rt△ABC中，∠C = 90°，a = 10，S_{△ABC} = $\frac{50}{3}\sqrt{3}$，则b = _______，∠A = _______.

答案： $\frac{10\sqrt{3}}{3}$@@60°@@解析：
∵ $S_{\triangle ABC}=\frac{1}{2}ab$，
∴ $\frac{1}{2}\times10b=\frac{50}{3}\sqrt{3}$。
∴ $b=\frac{10\sqrt{3}}{3}$。
∵ $\tan A=\frac{a}{b}=\frac{10}{\frac{10\sqrt{3}}{3}}=\sqrt{3}$，
∴ ∠A = 60°。

三、解答题
5. 在Rt△ABC中，∠C = 90°，a = 31，c = 31$\sqrt{2}$，解这个直角三角形.

答案： 解：
∵ ∠C = 90°，$a = 31$，$c = 31\sqrt{2}$，
∴ $b=\sqrt{c^{2}-a^{2}}=\sqrt{(31\sqrt{2})^{2}-31^{2}} = 31$。 又 $\sin A=\frac{a}{c}=\frac{31}{31\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$，
∴ ∠A = 45°，
∴ ∠B = 90° - ∠A = 90° - 45° = 45°。

6. 如图28 - 2 - 11所示，在△ABC中，AB = 1，AC = $\sqrt{2}$，sin B = $\frac{\sqrt{2}}{4}$，求BC的长.

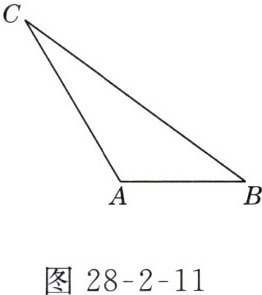
答案：
解：如图 D - 28 - 12 所示，过点 A 作 $AD\perp BC$，垂足为 D。 
∵ $\sin B=\frac{AD}{AB}$，
∴ $AD = AB\cdot\sin B = 1\times\frac{\sqrt{2}}{4}=\frac{\sqrt{2}}{4}$，
∴ $BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{1^{2}-(\frac{\sqrt{2}}{4})^{2}}=\frac{\sqrt{14}}{4}$。 在 $Rt\triangle ACD$ 中， $CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{2}}{4})^{2}}=\frac{\sqrt{30}}{4}$，
∴ $BC = CD + BD=\frac{\sqrt{30}}{4}+\frac{\sqrt{14}}{4}=\frac{\sqrt{30}+\sqrt{14}}{4}$。

7. 如图28 - 2 - 12所示，BC = 2，AC = $\sqrt{6}$，AB = $\sqrt{3}+1$，求△ABC各内角的度数.

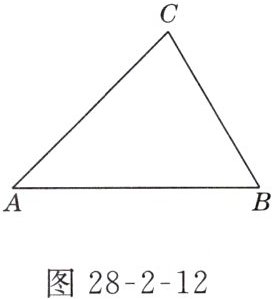
答案：
解：如图 D - 28 - 13 所示，过点 C 作 $CD\perp AB$ 于点 D。  设 $BD = x$，在 $Rt\triangle BCD$ 中，$CD^{2}=BC^{2}-BD^{2}=4 - x^{2}$。 在 $Rt\triangle ACD$ 中， $AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{(\sqrt{6})^{2}-(4 - x^{2})}=\sqrt{2 + x^{2}}$。
∵ $AD + BD = AB$，
∴ $\sqrt{2 + x^{2}}+x=\sqrt{3}+1$，
∴ $\sqrt{2 + x^{2}}=\sqrt{3}+1 - x$，
∴ $(\sqrt{2 + x^{2}})^{2}=(\sqrt{3}+1 - x)^{2}$，
∴ $2 + x^{2}=3 + 1 + x^{2}+2\sqrt{3}-2\sqrt{3}x - 2x$。
∴ $2\sqrt{3}x + 2x = 2 + 2\sqrt{3}$，
∴ $x = 1$，
∴ $\cos B=\frac{BD}{BC}=\frac{1}{2}$，
∴ ∠B = 60°， $AD=\sqrt{2 + x^{2}}=\sqrt{2 + 1}=\sqrt{3}$，
∴ $\cos A=\frac{AD}{AC}=\frac{\sqrt{3}}{\sqrt{6}}=\frac{\sqrt{2}}{2}$，
∴ ∠A = 45°，
∴ ∠ACB = 180° - ∠A - ∠B = 180° - 45° - 60° = 75°。
∴ $\triangle ABC$ 各内角的度数为 45°，60°，75°。