《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

5. 如图27-3-14所示，点B和点C之间的距离因有障碍不能直接测量，现测得AB = 25 m，AC = 20 m，∠BAC = 40°. 试按1∶1 000的比例尺画出△ABC，量出BC的长，求出实际的距离.

答案： 解：按 $1:1000$ 的比例尺分别计算出图上的距离为 $AB = 2.5\ cm$，$AC = 2\ cm$，用刻度尺、量角器画出符合条件的图形，测量 $BC\approx1.6\ cm$。（图略） 设实际距离为 $x\ cm$，根据题意，得 $\frac{1.6}{x}=\frac{1}{1000}$，解得 $x = 1600\ cm = 16\ m$。

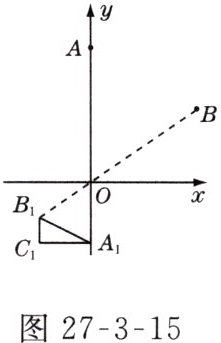
6. 如图27-3-15所示，在直角三角形A1B1C1中，∠C1 = 90°，点A，A1在y轴上，且AO = 2A1O，连接B1O并延长至B，使BO = 2B1O，请用尺规完成下列作图：连接C1O并延长到C，使CO = 2C1O，连接AB，BC，CA，则△A1B1C1 ________△ABC（填“≌”或“∽”），若∠B1A1C1 = 30°，A1(0，-1.5)，C1(-$\sqrt{3}$，-1.5)，求△ABC中边AB的长.

答案：
解：如图 D - 27 - 11 所示，$\triangle ABC$ 即为所作出的图形。 $\because\triangle ABC$ 与 $\triangle A_1B_1C_1$ 是位似图形，$\therefore\triangle A_1B_1C_1\sim\triangle ABC$。 $\because A_1(0,-1.5)$，$C_1(-\sqrt{3},-1.5)$，$\therefore A_1C_1=\sqrt{3}$。 $\because\angle B_1A_1C_1 = 30^{\circ}$，$A_1B_1 = 2B_1C_1$。 在 $Rt\triangle A_1B_1C_1$ 中，$A_1B_1^2 - B_1C_1^2 = A_1C_1^2 = 3$，$\therefore A_1B_1 = 2$。 $\because\triangle ABC$ 与 $\triangle A_1B_1C_1$ 是位似图形，$\therefore\triangle A_1OB_1\sim\triangle AOB$，$\therefore\frac{A_1B_1}{AB}=\frac{A_1O}{AO}=\frac{1}{2}$，$\therefore AB = 2A_1B_1 = 4$。故 $AB$ 的长是 4。 

1. 下列说法正确的是（ ）
A. 相似图形一定是位似图形
B. 对应点的连线相交于同一点的两个图形一定是位似图形
C. 位似图形一定是相似图形
D. 对应边互相平行的两个图形一定是位似图形

答案： C

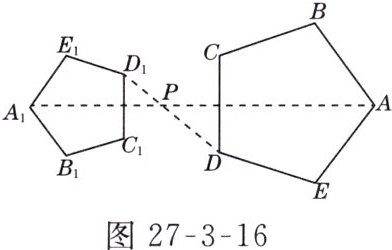
2. 如图27-3-16所示，五边形ABCDE和五边形A1B1C1D1E1是位似图形，且PA1 = $\frac{2}{3}$PA，则AB∶A1B1等于（ ）


A. $\frac{2}{3}$
B. $\frac{3}{2}$
C. $\frac{3}{5}$
D. $\frac{5}{3}$

答案： B

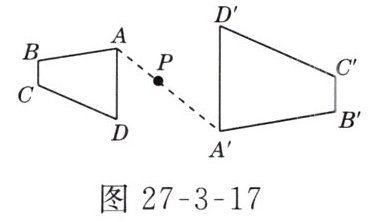
3. 如图27-3-17所示，四边形ABCD与四边形A'B'C'D'是两个以P为位似中心的位似图形，且PA∶PA' = 2∶3. 若四边形ABCD的面积为24 cm²，则四边形A'B'C'D'的面积为（ ）


A. 36 cm²
B. 40 cm²
C. 54 cm²
D. 48 cm²

答案： C

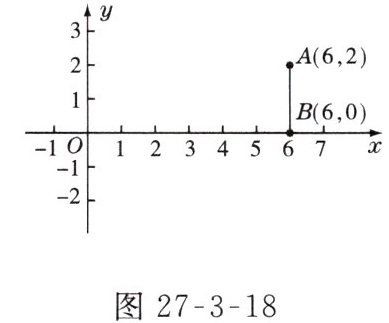
4. 如图27-3-18所示，在平面直角坐标系中有两点A(6,2)，B(6,0)，以原点为位似中心，相似比为1∶3，把线段AB缩小，则过点A对应点的反比例函数的解析式为（ ）


A. $y = \frac{4}{x}$
B. $y = \frac{4}{3x}$
C. $y = - \frac{4}{3x}$
D. $y = \frac{18}{x}$

答案： B