《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

3-1 已知：如图27-2-11所示，P是□ABCD的边BC延长线上的任一点，AP分别交BD和CD于点M和N，求证：AM² = MN·MP.

答案：

证明:
∵ AB∥DN,

∴ △AMB∽△NMD,
∴ $\frac{AM}{N}$ = $\frac{BM}{DM}$ .

又AD∥BP,
∴ △BMP∽△DMA,

∴ $\frac{MP}{AM}$ = $\frac{BM}{DM}$ .
∴ $\frac{AM}{MN}$ = $\frac{MP}{AM}$ ,

∴ AM=MN.MP.

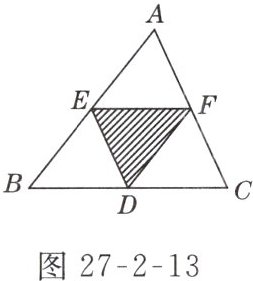
例4 一名学生做劳技作品，他把△ABC各边中点连接得到的△DEF涂色（如图27-2-13所示），试问涂色的三角形与原三角形相似吗？为什么？

答案：

4-1 在△ABC与△A'B'C'中，AB = 6，BC = 8，AC = 10，A'B' = 9，B'C' = 15，A'C' = 12. 试问△ABC与△A'B'C'相似吗？为什么？

答案：

解:相似.理由:

∵ A'B'− AB− $\frac{6}{9}$ = $\frac{2}{3}$ 'A'C"− BC− $\frac{8}{12}$ = $\frac{2}{3}$ ,

AC一 =

B'C= $\frac{10}{15}$ $\frac{2}{3}$ ,

.AB_BC_AC

",A'B'−A'C−B'C"

∴ △ABC∽△B'A'C'.