《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

2-1 下列各组线段中，成比例的是（ ）
A. 5 cm，6 cm，7 cm，8 cm
B. 3 cm，6 cm，2 cm，5 cm
C. 2 cm，4 cm，6 cm，8 cm
D. 12 cm，8 cm，15 cm，10 cm

答案： D@@解析：
∵$\frac{5}{6} \neq \frac{7}{8}$，$\frac{2}{3} \neq \frac{5}{6}$，$\frac{2}{4} \neq \frac{6}{8}$，$\frac{8}{10}=\frac{12}{15}=\frac{4}{5}$，
∴ A，B，C不是成比例线段，D是成比例线段。

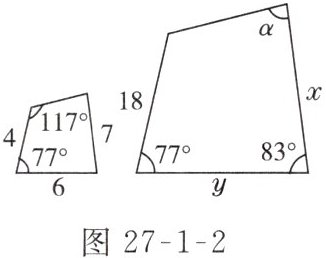
例 3 两个相似四边形如图 27-1-2 所示，求未知边 x，y 的长度和角α的大小.

答案： 解：由于两个四边形相似，
所以它们的对应边的比相等，对应角相等，
所以$\frac{18}{4}=\frac{y}{6}=\frac{x}{7}$，
解得 x = 31.5，y = 27，
α = 360° - （77° + 83° + 117°） = 83°.

3-1 如图 27-1-3 所示，已知四边形 ABCD 相似于四边形 A′B′C′D′，求四边形 A′B′C′D′的周长.

答案： 解：
∵ 四边形ABCD相似于四边形A'B'C'D'，
∴ $\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CD}{C'D'}=\frac{DA}{D'A'}$， 即$\frac{7}{A'B'}=\frac{5}{9}=\frac{6}{C'D'}=\frac{8}{D'A'}$，
∴ A'B' = 12.6，C'D' = 10.8，D'A' = 14.4，
∴ 四边形A'B'C'D'的周长 = 12.6 + 9 + 10.8 + 14.4 = 46.8。

1. 下列图形是相似图形的是（ ）
A. 两张孪生兄弟的照片
B. 三角板的内、外三角形
C. 行书中的“中”与楷书中的“中”
D. 同一棵树上摘下的两片树叶

答案： B@@解析：根据相似图形的定义，只有形状相同的两个图形才是相似图形。