《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

1. 小明在测量楼高时，先测出楼房落在地面上的影长BA为15 m（如图27 - 2 - 53所示），然后在A处树立一根高2 m的标杆，测得标杆的影长AC为3 m，则楼高为（ ）


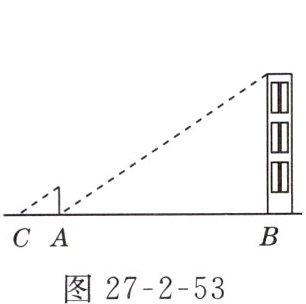
A. 10 m
B. 12 m
C. 15 m
D. 22.5 m

答案： A 解析：如图D - 27 - 6所示，由太阳光是平行光线可得△BAE∽△ACD，
∴$\frac{AB}{AC}=\frac{BE}{AD}$， 即$\frac{15}{3}=\frac{BE}{2}$，解得BE = 10.

2. 如图27 - 2 - 54所示，AB是斜靠在墙壁上的长梯，梯脚B距墙1.6 m，梯上点D距墙1.4 m，BD长0.55 m，则梯子的长为（ ）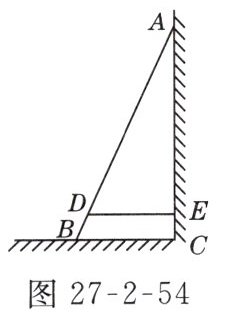
A. 3.85 m
B. 4.00 m
C. 4.40 m
D. 4.50 m

答案： C 解析：
∵DE//BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}=\frac{DE}{BC}$，即$\frac{AD}{AD + 0.55}=\frac{1.4}{1.6}$，
∴AD = 3.85 m，
∴梯子的长为3.85 + 0.55 = 4.40(m)， 故选C.

3. 赵亮同学想利用影长测量学校旗杆的高度，如图27 - 2 - 55所示，他在某一时刻测得直立在地面上1 m长的标杆其影长为1.2 m，同时旗杆的影子一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为9.6 m和2 m，则学校旗杆的高度为________m.

答案： 10

4. 如图27 - 2 - 56所示，小华在地面上放置一个平面镜E来测量铁塔AB的高度，镜子与铁塔的距离EB = 20 m，镜子与小华的距离ED = 2 m时，小华刚好从镜子中看到铁塔顶端点A，已知小华的眼睛距地面的高度CD = 1.5 m，则铁塔AB的高度是________m.

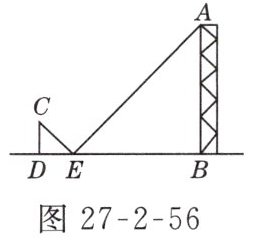
答案： 15

5. 如图27 - 2 - 57所示，小明想测量电线杆AB的高度，发现电线杆的影子恰好落在土坡的坡面和地面上，量得CD = 4 m，BC = 10 m，CD与地面成30°角，且此时测量1 m的标杆影长为2 m，求电线杆AB的高度.

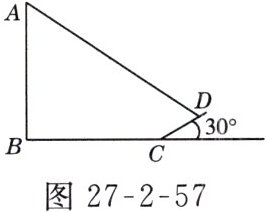
答案： 解：如图D - 27 - 7所示，延长AD交BC于点F，过点D作DE⊥BF于点E，
∵CD = 4 m，∠DCF = 30°，
∴DE = 2 m，CE = $2\sqrt{3}$ m. 由同一时刻物高与影长成正比，
∴$\frac{AB}{BF}=\frac{DE}{EF}=\frac{1}{2}$.
∴AB = $\frac{1}{2}BF$，DE = $\frac{1}{2}EF$，
∴EF = 4 m，
∴AB = $\frac{1}{2}(BC + CE + EF)=\frac{1}{2}(10 + 2\sqrt{3}+4)$ = $7+\sqrt{3}$(m)， 即电线杆AB的高为$(7+\sqrt{3})$m.