《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

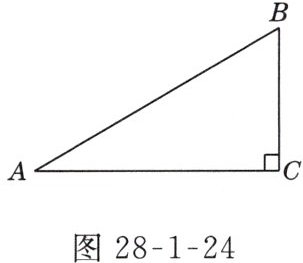
2. 如图28-1-24，在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$AB = 2BC$，则$\sin B$的值为（ ）

A. $\frac{1}{2}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{\sqrt{3}}{2}$
D. 1

答案： C

3. 已知$\angle A$为锐角，且$\cos A=\frac{\sqrt{3}}{2}$，则$\angle A$的度数为______.

答案： 30º

4. 如图28-1-25所示，在$\triangle ABC$中，$\angle C = 90^{\circ}$，$BC = 4\ cm$，$\tan B=\frac{3}{2}$，则$\triangle ABC$的面积是______$cm^{2}$.

答案： 12

5. 求值：
（1）$\frac{1}{2}\sin 60^{\circ}-\frac{\sqrt{2}}{2}\sin 45^{\circ}+\sqrt{2}\cos 45^{\circ}\sin 30^{\circ}$；
（2）$\frac{\sin 45^{\circ}+\cos 30^{\circ}}{3 - 2\cos 60^{\circ}}-\sin 30^{\circ}\tan 30^{\circ}$.

答案：

解:
(1)原式= $\frac{1}{2}$ × $\frac{\sqrt{3}}{2}$ 一 $\frac{\sqrt{2}}{2}$ × $\frac{\sqrt{2}}{2}$ + $\sqrt{2}$ ×

$\frac{\sqrt{2}}{2}$ × $\frac{1}{2}$ = $\frac{\sqrt{3}}{4}$ − $\frac{1}{2}$ + $\frac{1}{2}$ = $\frac{\sqrt{3}}{4}$

$\frac{\sqrt{2}}{2}$ + $\frac{\sqrt{3}}{2}$

(2)原式= 3−2× $\frac{1}{2}$  $\frac{1}{2}$ × $\frac{\sqrt{3}}{3}$ = $\frac{\sqrt{2}}{4}$ + $\frac{\sqrt{3}}{4}$ 一

$\frac{\sqrt{3}}{6}$ = $\frac{\sqrt{2}}{4}$ + $\frac{\sqrt{3}}{12}$ .

1. $\sqrt{(1 - \tan 60^{\circ})^{2}}-\cos 30^{\circ}$等于（ ）
A. $\frac{\sqrt{3}}{2}-1$
B. $\frac{\sqrt{3}}{2}+1$
C. $\frac{3\sqrt{3}}{2}-1$
D. $1-\frac{3\sqrt{3}}{2}$

答案： A

2. 在$\triangle ABC$中，$\angle A = 120^{\circ}$，$AB = 4$，$AC = 2$，则$\sin B$的值是（ ）
A. $\frac{5\sqrt{7}}{14}$
B. $\frac{\sqrt{3}}{5}$
C. $\frac{\sqrt{21}}{7}$
D. $\frac{\sqrt{21}}{14}$

答案： D

3. 若$\sqrt{3}\tan(\alpha + 10^{\circ}) = 1$，则锐角$\alpha$等于______.

答案： 20º

4. 在锐角$\triangle ABC$中，若$\angle A$，$\angle B$满足$\vert\cos A - \frac{1}{2}\vert+(\sin B - \frac{\sqrt{2}}{2})^{2}=0$，则有$\angle C =$______.

答案： 75º

5. 化简：$\sqrt{\sin^{2}A - 2\sin A + 1}=$______.

答案： 1-sin A

6. 在$\triangle ABC$中，$AB = 2$，$AC = \sqrt{2}$，$\angle B = 30^{\circ}$，则$\angle BAC$的度数是______.

答案： 105º或15º

7. 计算：
（1）$\sin 60^{\circ}\tan 30^{\circ}+\cos^{2}45^{\circ}$；
（2）$\frac{3\cos 30^{\circ}}{5\sin 30^{\circ}-1}-\vert-\tan 60^{\circ}\vert$.

答案： 1
0

8. 若$\tan^{2}\alpha + 4\tan\alpha - 5 = 0$，求锐角$\alpha$.

答案： 45º