第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 相似三角形对应高的比、对应中线的比与对应角平分线的比都等于________.
答案:
相似比
2. 相似三角形周长的比等于________.
答案:
相似比
3. 相似三角形________等于相似比的平方.
答案:
面积的比
4. 根据预习内容,回答下列问题.
如图27 - 2 - 44所示,身高1.6 m的学生小李想测量学校的旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC = 2 m,BC = 8 m,则旗杆的高度是( )
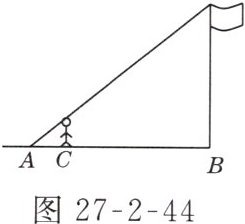
A. 6.4 m
B. 7 m
C. 8 m
D. 9 m
如图27 - 2 - 44所示,身高1.6 m的学生小李想测量学校的旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC = 2 m,BC = 8 m,则旗杆的高度是( )

A. 6.4 m
B. 7 m
C. 8 m
D. 9 m
答案:
C 解析:设旗杆的高度为h m,由题意得$\frac{1.6}{h}=\frac{2}{2 + 8}$,解得h = 8.
例1 如图27 - 2 - 45所示,要测量河两岸相对的两点A,B间的距离,从B处与AB成90°方向出发,向右走50 m到C处立一根标杆,然后方向不变继续朝右走10 m到达D处,在D处顺时针旋转90°,沿该方向再走17 m,到达E处,此时A(目标),C(标杆)与E在同一直线上,求A,B间的距离.
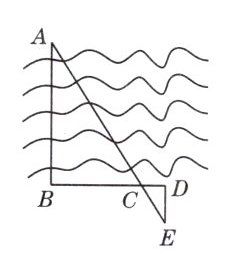

答案:
解:由题意得∠B = ∠D = 90°,
∠ACB = ∠DCE,
所以△ABC∽△EDC,所以$\frac{AB}{DE}=\frac{BC}{CD}$,
所以$AB=\frac{BC\cdot DE}{CD}=\frac{50×17}{10}=85$(m).
答:A,B间的距离为85 m.
∠ACB = ∠DCE,
所以△ABC∽△EDC,所以$\frac{AB}{DE}=\frac{BC}{CD}$,
所以$AB=\frac{BC\cdot DE}{CD}=\frac{50×17}{10}=85$(m).
答:A,B间的距离为85 m.
例2 如图27 - 2 - 46所示,为了测量一棵树CD的高度,测量者在B点立一高为2 m的标杆,观测者在F处时,观测者的眼睛E与杆顶A和树顶C在同一条直线上. 若测量BD = 6.4 m,FB = 1.6 m,EF = 1.6 m,求树高.
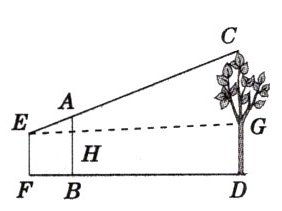

答案:
解:由题意得∠B = ∠D = 90°,
∠ACB = ∠DCE,
所以△ABC∽△EDC,所以$\frac{AB}{DE}=\frac{BC}{CD}$,
所以$AB=\frac{BC\cdot DE}{CD}=\frac{50×17}{10}=85$(m).
答:A,B间的距离为85 m.
∠ACB = ∠DCE,
所以△ABC∽△EDC,所以$\frac{AB}{DE}=\frac{BC}{CD}$,
所以$AB=\frac{BC\cdot DE}{CD}=\frac{50×17}{10}=85$(m).
答:A,B间的距离为85 m.
查看更多完整答案,请扫码查看


