《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

6. 如图27-2-21所示，∠DAB = ∠CAE，请你再补充一个条件， ，使得△ABC∽△ADE，并说明理由.

答案：

解:(答案不唯一) $\frac{AB}{D}$ = $\frac{AC}{E}$ ,理由:

∵ ∠DAB=∠CAE,

∴ ∠DAE=∠BAC.

又 $\frac{AB}{D}$ = $\frac{AC}{E}$ ,
∴ △ABC∽△ADE.

7. 如图27-2-22所示，一条河的两岸有一段是平行的，在河的南岸边每隔5 m有一棵树，在北岸边每隔50 m有一根电线杆. 小丽站在离南岸边25 m的点O处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，求河宽.

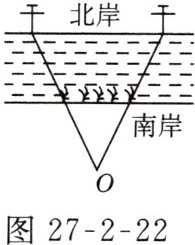
答案：

两根电线杆，C,D是两棵树,它们之间还有3棵树,故CD=4×5=20(m),

OE=25m,

∵ CD∥AB, 0

∴ △OCD∽△OAB, 图D−27−2

△OCE∽△OAF,

∴ $\frac{OC}{A}$ = $\frac{CD}{B}$ , $\frac{OC}{OA}$ = $\frac{OE}{OF}$ ..
∴ $\frac{OE}{F}$ = $\frac{CD}{B}$ 9

即 $\frac{25}{25+EF}$ = $\frac{20}{50}$ ,解得EF=37.5.

答:河宽为37.5m.

8. 如图27-2-23所示，O为△ABC内一点，A'，B'，C'分别在OA，OB，OC上，且A'B'//AB，B'C'//BC，A'C'//AC. 求证：△ABC∽△A'B'C'.

答案：

证明:
∵ A'B'∥AB,

∴ △OA'B∽△OAB,
∴ $\frac{A'B}{AB}$ = $\frac{OB}{OB}$ .

同理 $\frac{B'C}{BC}$ $\frac{OB}{OB}$ $\frac{OC'}{OC}$ , $\frac{A'C}{AC}$ $\frac{OC'}{OC}$ .

∴ $\frac{A'B}{AB}$ = $\frac{B'C}{BC}$ = $\frac{A'C}{AC}$ ,

∴ △ABC∽△A'B'C'

1. 如图27-2-24所示，已知DE//BC，下列各等式错误的是（ ）

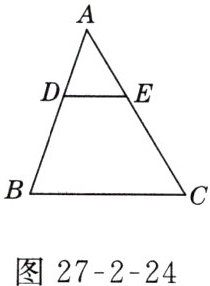
A. $\frac{AD}{DB}=\frac{AE}{EC}$
B. $\frac{AD}{AB}=\frac{DE}{BC}$
C. $\frac{AD}{AB}=\frac{AE}{AC}$
D. $\frac{AD}{AE}=\frac{AC}{AB}$

答案： D

2. 甲三角形的三边长分别为1，$\sqrt{2}$，$\sqrt{5}$，乙三角形的三边长分别为5，$\sqrt{5}$，$\sqrt{10}$，则甲、乙两个三角形（ ）
A. 一定相似
B. 一定不相似
C. 不一定相似
D. 无法判断是否相似

答案： A

3. 在△ABC和△A'B'C'中，已知AB·B'C' = BC·A'B'，若使△ABC∽△A'B'C'，还应增加的条件是（ ）
A. AC = A'C'
B. ∠A = ∠A'
C. ∠B = ∠B'
D. ∠C = ∠C'

答案： C