《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

1. 一般地，设在某个变化过程中有两个变量$x,y$，如果对$x$在某一范围内的每一个确定的值，$y$都有______确定的值与它对应，那么就说$y$是$x$的函数，$x$是______.

答案： 唯一@@自变量

2. 直角三角形中两锐角______.

答案： 互余

3. 在直角三角形中，两直角边的______等于斜边的______.

答案： 平方和@@平方

4. 在直角三角形$ABC$中，$\angle C = 90^{\circ}$，当$\angle A$是任意一个确定的锐角时，它的对边与斜边的比是一个______值，也就是说，当$\angle A$的度数一定时，这个值与三角形的______无关.

答案： 固定@@大小

5. 在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，我们把锐角$A$的______与______的比叫作$\angle A$的正弦.

答案： 对边@@斜边

6. 根据预习内容，回答下列问题.
（1）在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$AB = 13$，$AC = 12$，则$\sin B$的值为（ ）
A. $\frac{12}{13}$ B. $\frac{5}{13}$ C. $\frac{5}{12}$ D. $\frac{12}{5}$
（2）将$Rt\triangle ABC$的各边都扩大2倍得到$Rt\triangle A'B'C'$，已知$\angle C = 90^{\circ}$，那么锐角$A$，$A'$的正弦值的关系为（ ）
A. $\sin A=\sin A'$ B. $\sin A = 2\sin A'$ C. $2\sin A=\sin A'$ D. 不确定

答案： （1）A 解析：
∵∠C = 90°，AB = 13，AC = 12，
∴sin B = $\frac{AC}{AB}=\frac{12}{13}$。 （2）A 解析：
∵sin A = $\frac{BC}{AB}$，sin A' = $\frac{B'C'}{A'B'}=\frac{2BC}{2AB}=\frac{BC}{AB}$，
∴sin A = sin A'。

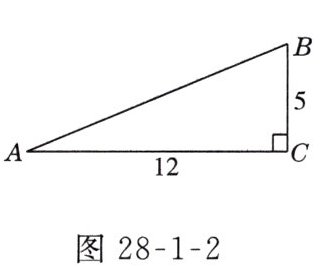
例1 如图28-1-2所示，在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，求$\sin A$和$\sin B$的值.

答案： 解：$\because\angle C = 90^{\circ}$，
$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{12^{2}+5^{2}} = 13$.
$\therefore\sin A=\frac{BC}{AB}=\frac{5}{13}$，$\sin B=\frac{AC}{AB}=\frac{12}{13}$.

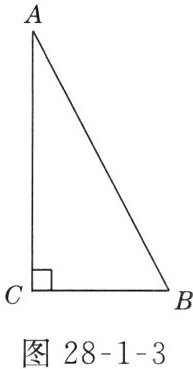
例2 在直角三角形中，一直角边长为30，此边所对角的正弦值为$\frac{15}{17}$，求这个三角形的周长和面积.

答案： 解：如图28-1-3所示，
$\angle C = 90^{\circ}$，$AC = 30$，
则$\sin B=\frac{15}{17}$.
$\because\sin B=\frac{AC}{AB}$，$\therefore\frac{30}{AB}=\frac{15}{17}$.
$\therefore AB = 34$.
$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{34^{2}-30^{2}} = 16$.
$\therefore\triangle ABC$的周长为$AC + BC + AB = 30 + 16 + 34 = 80$，
$\triangle ABC$的面积$S=\frac{1}{2}AC\cdot BC=\frac{1}{2}\times30\times16 = 240$.