《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

4. 为了预防流感，某学校对教室用药熏消毒法进行消毒. 已知药物燃烧时，室内空气中每立方米的含药量$y$（单位：mg）与时间$x$（单位：min）成正比例，药物燃烧完后$y$与$x$成反比例，如图26 - 2 - 7所示. 观测得药物8min燃烧完毕，此时室内空气中每立方米的含药量为6mg. 请根据题中提供的信息，解答下列问题.
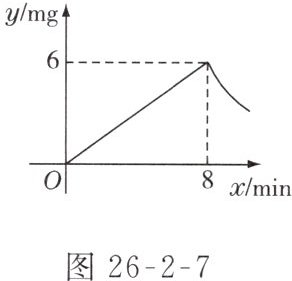
（1）药物燃烧时，$y$关于$x$的函数解析式为______，自变量的取值范围是________；药物燃烧完后，$y$关于$x$的函数解析式为__________.
（2）研究表明，当空气中每立方米的含药量低于1.6mg时，学生方可进入教室，那么从开始消毒，至少要经过________min后，学生才能回到教室.
（3）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？

答案： $y = \frac{3}{4}x$@@$0\leq x\leq8$@@$y = \frac{48}{x}(x＞8)$@@30@@解： （3）本次消毒有效。理由：把$y = 3$分别代入$y = \frac{3}{4}x$，$y = \frac{48}{x}$中，求得$x_1 = 4$，$x_2 = 16$，而$16 - 4 = 12＞10$，即空气中每立方米的含药量不低于$3\ mg$的持续时间为$12\ min$，所以这次消毒有效。

5. 张先生以按揭方式（首付一部分，剩余部分按每月分期付款）购买了价格为16万元的汽车，交了首付款之后每月付款$y$元，$x$个月结清. $y$与$x$的函数关系如图26 - 2 - 8所示，试根据图象提供的信息解答下列问题.
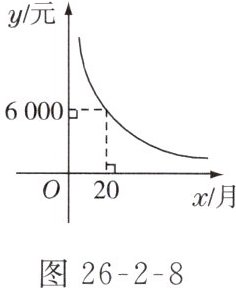
（1）确定$y$与$x$的函数解析式，并求出首付款的数目.
（2）张先生若打算120个月结清余款，每月应付多少元？
（3）若打算每月付款不超过1500元，则张先生至少几个月才能结清余款？

答案： 解： （1）由图象知，$y$与$x$成反比例。设$y$与$x$的函数解析式为$y = \frac{k}{x}(k\neq0)$。因为反比例函数$y = \frac{k}{x}$的图象过点$(20,6000)$，所以$k = 20×6000 = 120000$。所以$y$与$x$的函数解析式为$y = \frac{120000}{x}(x＞0)$。所以首付款为$160000 - 120000 = 40000$（元）。 （2）当$x = 120$时，$y = \frac{120000}{120} = 1000$（元）。故若打算120个月结清余款，每月应付1000元。 （3）当$y\leq1500$，即$\frac{120000}{x}\leq1500$时，解得$x\geq80$，即张先生至少80个月才能结清余款。