第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
3. 把一个矩形对折,得到的矩形与原矩形相似,则这个矩形的长、宽之比为( )
A. 2:1
B. 4:1
C. $\sqrt{2}$:1
D. 3:2
A. 2:1
B. 4:1
C. $\sqrt{2}$:1
D. 3:2
答案:
C@@解析:设原矩形的长为a,宽为b,根据题意,得$\frac{a}{b}=\frac{b}{\frac{1}{2}a}$,
$\frac{1}{2}a^{2}=b^{2}$,$\frac{a^{2}}{b^{2}}=2$,$\frac{a}{b}=\sqrt{2}$,
∴ 原矩形的长、宽之比为$\sqrt{2}$ : 1。
∴ 原矩形的长、宽之比为$\sqrt{2}$ : 1。
4. 一个多边形的边长分别为 2,3,4,5,6,另一个多边形和这个多边形相似,其最短边长为 6,则最长边长为( )
A. 12
B. 18
C. 24
D. 30
A. 12
B. 18
C. 24
D. 30
答案:
B@@解析:设最长边长为x,
∵ 相似多边形对应边的比相等,
∴ $\frac{2}{6}=\frac{6}{x}$,
∴ x = 18。
∵ 相似多边形对应边的比相等,
∴ $\frac{2}{6}=\frac{6}{x}$,
∴ x = 18。
5. 下列各组图形中,一定相似的是( )
A. 底角为 20°的两个等腰梯形
B. 邻边之比为 1:2 的两个平行四边形
C. 各有一个角是 20°的两个平行四边形
D. 两条邻边对应成比例的两个矩形
A. 底角为 20°的两个等腰梯形
B. 邻边之比为 1:2 的两个平行四边形
C. 各有一个角是 20°的两个平行四边形
D. 两条邻边对应成比例的两个矩形
答案:
D@@解析:底角为20°的两个等腰梯形的四个角对应相等,但四条边的比不一定相等,故A错;邻边之比为1 : 2的两个平行四边形的四条边的比相等,但四个角不一定相等,故B错;各有一个角是20°的两个平行四边形的四个角对应相等,但四条边的比不一定相等,故C错;两条邻边对应成比例的两个矩形的四条边的比相等,两个矩形的四个角也对应相等,故D正确。
6. 如图 27-1-6 所示,在矩形 ABCD 中,AB = 1,在 BC 上取一点 E,沿 AE 将△ABE 向上折叠,使 B 点落在 AD 上的 F 点,若四边形 EFDC 与矩形 ABCD 相似,则 AD =( )
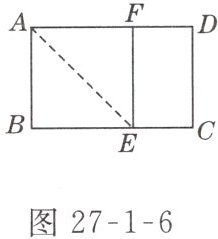
A. $\frac{\sqrt{5}-1}{2}$
B. $\frac{1+\sqrt{5}}{2}$
C. $\sqrt{3}$
D. 2

A. $\frac{\sqrt{5}-1}{2}$
B. $\frac{1+\sqrt{5}}{2}$
C. $\sqrt{3}$
D. 2
答案:
B@@解析:AB = 1,设AD = x,则FD = x - 1,FE = 1,
∵ 矩形EFDC与矩形ABCD相似,
∴ $\frac{EF}{FD}=\frac{AD}{AB}$,即$\frac{1}{x - 1}=\frac{x}{1}$,解得$x_{1}=\frac{1 + \sqrt{5}}{2}$,$x_{2}=\frac{1 - \sqrt{5}}{2}$(负值,舍去),经检验$x=\frac{1 + \sqrt{5}}{2}$是原方程的解,故选B。
∵ 矩形EFDC与矩形ABCD相似,
∴ $\frac{EF}{FD}=\frac{AD}{AB}$,即$\frac{1}{x - 1}=\frac{x}{1}$,解得$x_{1}=\frac{1 + \sqrt{5}}{2}$,$x_{2}=\frac{1 - \sqrt{5}}{2}$(负值,舍去),经检验$x=\frac{1 + \sqrt{5}}{2}$是原方程的解,故选B。
二、填空题
7. 已知线段 AB 的长为 15,点 C 在线段 AB 的延长线上,且 AC:BC = 3:2,则 BC 的长为_________.
7. 已知线段 AB 的长为 15,点 C 在线段 AB 的延长线上,且 AC:BC = 3:2,则 BC 的长为_________.
答案:
30@@解析:由题意知,AC = AB + BC,
∵ AC : BC = 3 : 2,
∴ (AB + BC) : BC = 3 : 2, 即(15 + BC) : BC = 3 : 2,
∴ BC = 30。
∵ AC : BC = 3 : 2,
∴ (AB + BC) : BC = 3 : 2, 即(15 + BC) : BC = 3 : 2,
∴ BC = 30。
8. 在 1:500 000 的地图上,量得甲、乙两城市之间的直线距离为 15 cm,那么这两个城市之间的实际距离是 ____________ km.
答案:
75@@解析:设实际距离为x cm,
则1 : 500 000 = 15 : x,
∴ x = 7 500 000,7 500 000 cm = 75 km。
∴ x = 7 500 000,7 500 000 cm = 75 km。
三、解答题
9. 已知四条线段的长度为 a = 2 cm,b = 30 m,c = 6 cm,d = 10 m,请判断它们是不是成比例线段.
9. 已知四条线段的长度为 a = 2 cm,b = 30 m,c = 6 cm,d = 10 m,请判断它们是不是成比例线段.
答案:
解:
∵ a = 2 cm,b = 30 m = 3 000 cm,c = 6 cm,d = 10 m = 1 000 cm,
∴ a < c < d < b。
∵ $\frac{a}{c}=\frac{2}{6}=\frac{1}{3}$,$\frac{d}{b}=\frac{1 000}{3 000}=\frac{1}{3}$,
∴ $\frac{a}{c}=\frac{d}{b}$。
∴ 它们是成比例线段。
∵ a = 2 cm,b = 30 m = 3 000 cm,c = 6 cm,d = 10 m = 1 000 cm,
∴ a < c < d < b。
∵ $\frac{a}{c}=\frac{2}{6}=\frac{1}{3}$,$\frac{d}{b}=\frac{1 000}{3 000}=\frac{1}{3}$,
∴ $\frac{a}{c}=\frac{d}{b}$。
∴ 它们是成比例线段。
10. 如图 27-1-7 所示,把矩形 ABCD 对折,折痕为 MN,矩形 DMNC 与矩形 ABCD 相似,已知 AB = 4.
(1)求 AD 的长;
(2)求矩形 DMNC 与矩形 ABCD 的相似比.
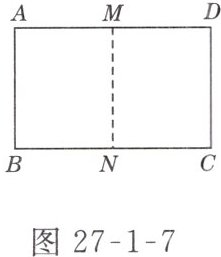
(1)求 AD 的长;
(2)求矩形 DMNC 与矩形 ABCD 的相似比.

答案:
解:(1)由已知,得
MN = AB,MD = $\frac{1}{2}$AD = $\frac{1}{2}$BC。
∵ 矩形DMNC与矩形ABCD相似,
∴ $\frac{DM}{AB}=\frac{MN}{BC}$,即$\frac{1}{2}AD^{2}=AB^{2}$,由AB = 4得,AD = $4\sqrt{2}$。 (2)矩形DMNC与矩形ABCD的相似比为$\frac{DM}{AB}=\frac{\sqrt{2}}{2}$。
∵ 矩形DMNC与矩形ABCD相似,
∴ $\frac{DM}{AB}=\frac{MN}{BC}$,即$\frac{1}{2}AD^{2}=AB^{2}$,由AB = 4得,AD = $4\sqrt{2}$。 (2)矩形DMNC与矩形ABCD的相似比为$\frac{DM}{AB}=\frac{\sqrt{2}}{2}$。
查看更多完整答案,请扫码查看


