《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

2. 下列说法中不正确的是（ ）
A. 我国国旗上的大五角星和小五角星是相似图形
B. 放大镜下的三角形与原来的三角形是相似图形
C. 平面镜中你的像与你本人是相似的
D. “哈哈镜”中人的像与本人是相似的

答案： D@@解析：A、B、C选项中的两个图形都是相似的。D选项“哈哈镜”中人的像与本人是不相似的。

3. 已知 A，B 两地的实际距离是 250 m，若画在图上的距离是 5 cm，则图上距离与实际距离的比是（ ）
A. 1：50
B. 1：5 000
C. 1：500
D. 1：50 000

答案： B@@解析：求两条线段的比时要注意单位统一，250 m = 25 000 cm，所以图上距离与实际距离的比为5 : 25 000 = 1 : 5 000。

4. 下列四组线段中，不成比例的是（ ）
A. a = 3，b = 6，c = 2，d = 4
B. a = 1，b = $\sqrt{2}$，c = $\sqrt{3}$，d = $\sqrt{6}$
C. a = 4，b = 6，c = 5，d = 10
D. a = $\sqrt{2}$，b = $\sqrt{3}$，c = 2，d = $\sqrt{6}$

答案： C@@解析：判断四条线段是否成比例的方法是看两条较短线段的比是否等于两条较长线段的比。 A中$\frac{c}{a}=\frac{2}{3}$，$\frac{d}{b}=\frac{4}{6}=\frac{2}{3}$，
∴ $\frac{c}{a}=\frac{d}{b}$，
∴ A中四条线段成比例； B中$\frac{a}{b}=\frac{1}{\sqrt{2}}$，$\frac{c}{d}=\frac{\sqrt{3}}{\sqrt{6}}=\frac{1}{\sqrt{2}}$，
∴ $\frac{a}{b}=\frac{c}{d}$，
∴ B中四条线段成比例； C中$\frac{a}{c}=\frac{4}{5}$，$\frac{b}{d}=\frac{6}{10}=\frac{3}{5}$，
∴ $\frac{a}{c} \neq \frac{b}{d}$，
∴ C中四条线段不成比例； D中$\frac{a}{b}=\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}$，$\frac{c}{d}=\frac{2}{\sqrt{6}}=\frac{\sqrt{6}}{3}$，
∴ $\frac{a}{b}=\frac{c}{d}$，
∴ D中四条线段成比例。故选C。

5. 下列说法中正确的是（ ）
A. 有一个角是 30°的两个等腰三角形相似
B. 任意两个等腰梯形相似
C. 任意两个矩形相似
D. 各有一个角是 150°的两个等腰三角形相似

答案： D@@解析：若一个等腰三角形的顶角为30°，另一个等腰三角形的底角为30°，则这两个等腰三角形的三个角不对应相等，故A错；任意两个等腰梯形的角不一定对应相等，故B错；任意两个矩形的四个角虽然对应相等，但四条边的比不一定相等，故C错，所以选D。

6. 如图 27-1-4 所示，四边形 ABCD 与四边形 EFGH 相似吗？说明理由.

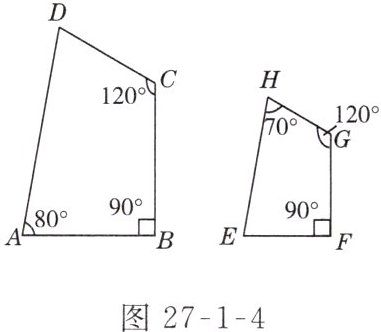
答案： 解：无法判定两个四边形是否相似，因为虽然能得到各对应角都相等，但依据条件无法判定对应边的比是否相等，故无法判定是否相似。

7. 已知 a，b，c 为△ABC 的三边，并且 a + b + c = 60 cm，$\frac{a}{3}=\frac{b}{4}=\frac{c}{5}$，试求△ABC 三边的长.

答案： 解：
∵ $\frac{a}{3}=\frac{b}{4}=\frac{c}{5}$，
∴ $\frac{a + b + c}{3 + 4 + 5}=\frac{a}{3}$， 即$\frac{60}{12}=\frac{a}{3}$，
∴ a = 15。 同理，$\frac{60}{12}=\frac{b}{4}$，$\frac{60}{12}=\frac{c}{5}$，
∴ b = 20，c = 25。
∴ 三角形三边的长为15 cm，20 cm，25 cm。

一、选择题
1. 小明的文具袋里有一塑料的等腰直角三角板，教室的讲台上有一木制的大的等腰直角三角板，那么这两个三角板（ ）
A. 相似
B. 边长不成比例
C. 不相似
D. 无法比较

答案： A

2. 如果线段上一点 P 把线段分割为两条线段 PA，PB，当$PA^{2}=PB·AB$，即 PA≈0.618AB 时，称点 P 是线段 AB 的黄金分割点. 现已知线段 AB = 10，点 P 是线段 AB 的黄金分割点，如图 27-1-5 所示，那么线段 PB 的长约为（ ）

A. 6.18
B. 0.382
C. 0.618
D. 3.82

答案： D@@解析：
∵ PA ≈ 0.618AB，
∴ PB ≈ 0.382AB = 0.382×10 = 3.82。