《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

跟踪训练
3-1 如图27-3-10所示，将图中的△ABC作下列运动，作出相应的图形，并指出三个顶点所发生的变化.
（1）沿y轴负半轴平移3个单位长度；
（2）关于y轴对称；
（3）以点B为位似中心按相似比2扩大.

答案：
解：（1）如图 D - 27 - 9 所示，将 $\triangle ABC$ 沿 $y$ 轴负方向平移 3 个单位长度后得到 $\triangle A_1B_1C_1$，$A_1(0,-5)$，$B_1(3,-4)$，$C_1(2,-2)$，即横坐标不变，纵坐标减 3。 （2）如图 D - 27 - 9 所示，$\triangle ABC$ 关于 $y$ 轴对称得到 $\triangle A_2B_2C_2$，$A_2(0,-2)$，$B_2(-3,-1)$，$C_2(-2,1)$，即纵坐标不变，横坐标变为原来的相反数。 （3）如图 D - 27 - 9 所示，将 $\triangle ABC$ 以点 $B$ 为位似中心，按相似比 2 放大后，得到 $\triangle A_3B_3C_3$ 和 $\triangle A_4B_4C_4$。 当两图形在位似中心的同侧时，得到 $\triangle A_3B_3C_3$，可求得 $A_3(-3,-3)$，$B_3(3,-1)$，$C_3(1,3)$。 当两图形分居位似中心的两侧时，得到 $\triangle A_4B_4C_4$，可求得 $A_4(9,1)$，$B_4(3,-1)$，$C_4(5,-5)$。 

1. 下列图形中，△ADE∽△ABC，则△ADE与△ABC具有位似关系的是（ ）

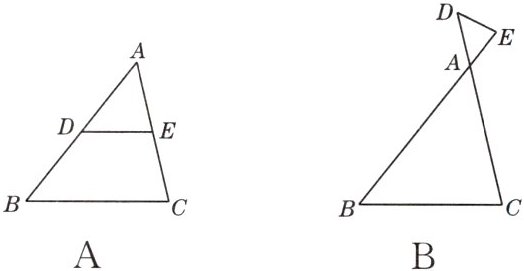
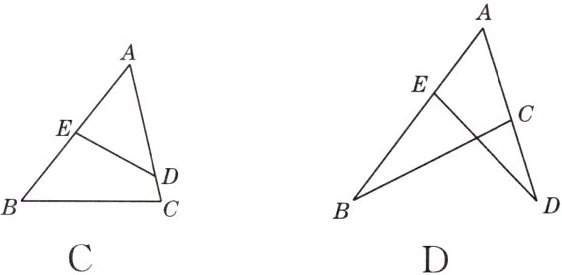
答案： A

2. 如图27-3-11所示，已知△EFH和△MNK是位似图形，那么其位似中心是（ ）


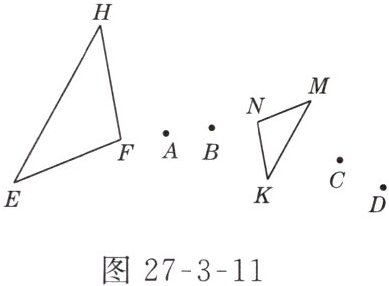
A. 点A
B. 点B
C. 点C
D. 点D

答案： B

3. 如图27-3-12所示，正方形OABC与正方形ODEF是位似图形，点O为位似中心，相似比为1∶$\sqrt{2}$，点A的坐标为(0,1)，则点E的坐标是 ________.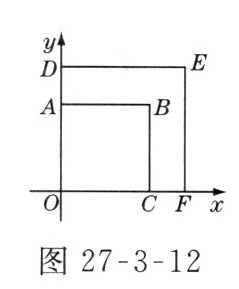

答案： $(\sqrt{2},\sqrt{2})$

4. 如图27-3-13所示，以O为位似中心，将△ABC按相似比$\frac{1}{2}$缩小，并简要写出画法.

答案：
解：如图 D - 27 - 10 所示， 画法：（1）分别连接 $OA$，$OB$，$OC$。 （2）分别取 $OA$，$OB$，$OC$ 的中点为 $A'$，$B'$，$C'$。 （3）顺次连接 $A'B'$，$B'C'$，$C'A'$。$\triangle A'B'C'$ 就是所要画的图形。