《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

2. 如图27 - 2 - 50所示，A，B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够，于是他想了一个办法：在地上取一点C，使它可以直接到达A，B两点，在AC的延长线上取一点D，使$CD=\frac{1}{2}CA$，在BC的延长线上取一点E，使$CE=\frac{1}{2}CB$，测得DE的长为5 m，则AB两点间的距离为（ ）

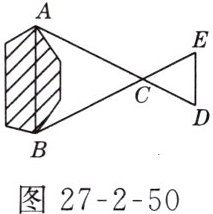
A. 6 m
B. 8 m
C. 10 m
D. 12 m

答案： C 解析：在△ABC和△DEC中，
∵$\frac{CD}{CA}=\frac{CE}{CB}=\frac{1}{2}$，且∠ACB = ∠DCE，
∴△ABC∽△DEC，
∴$\frac{DE}{AB}=\frac{1}{2}$. 又DE = 5 m，
∴AB = 10 m.

3. 如图27 - 2 - 51所示，AB和DE是直立在地面上的两根立柱，AB = 5 m，某一时刻，AB在阳光下的投影BC = 4 m.
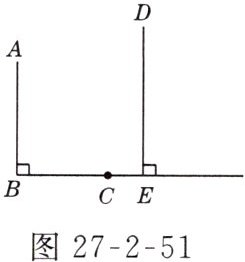
（1）请你在图中画出此时DE在阳光下的投影，并简述画图步骤；
（2）在测量AB的投影长时，同时测得DE在阳光下的投影长为6 m，请你计算DE的长.

答案： 解：
(1)如图D - 27 - 4所示，连接AC，过点D作DF//AC，交直线BE于F，则EF就是DE的投影.
(2)
∵太阳光线是平行的，
∴AC//DF，
∴∠ACB = ∠DFE. 又∠ABC = ∠DEF = 90°，
∴△ABC∽△DEF，
∴$\frac{AB}{DE}=\frac{BC}{EF}$.
∵AB = 5 m，BC = 4 m，EF = 6 m，
∴$\frac{5}{DE}=\frac{4}{6}$，
∴DE = 7.5(m).

4. 某市经济开发区建有B，C，D三个食品加工厂，这三个工厂和开发区A处的自来水厂正好在一个矩形的四个顶点上，它们之间有公路相通，且AB = CD = 900 m，AD = BC = 1700 m. 自来水公司已经修好一条自来水主管道AN，B，C两厂之间的公路与自来水管道交于E处，EC = 500 m. 若修建自来水主管道到各工厂的费用由各厂负担，已知管道每米造价800元.
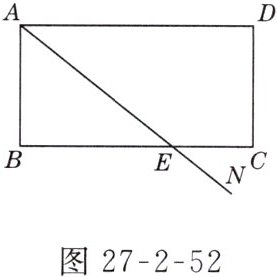
（1）要使修建自来水管道的造价最低，这三个工厂的自来水管道路线应怎样设计？并在图27 - 2 - 52中画出.
（2）求出各厂所修建自来水管道的最低造价各是多少元？

答案： 解：
(1)如图D - 27 - 5所示，过B，C，D分别作AN的垂线BH，CF，DG交AN于H，F，G，则BH，CF，DG即为所求的造价最低的管道路线.
(2)在Rt△ABE中，BE = BC - CE = 1200 m，
∴AE = $\sqrt{AB^{2}+BE^{2}}$ = $\sqrt{900^{2}+1200^{2}}$ = 1500(m). 由△ABE∽△CFE，得$\frac{CF}{AB}=\frac{CE}{AE}$，
∴CF = $\frac{CE\cdot AB}{AE}=\frac{500×900}{1500}$ = 300(m). 由△BHE∽△CFE，得$\frac{CF}{BH}=\frac{CE}{BE}$，
∴BH = $\frac{BE\cdot CF}{CE}=\frac{1200×300}{500}$ = 720(m). 由△ABE∽△DGA，得$\frac{AB}{DG}=\frac{AE}{AD}$，
∴DG = $\frac{AB\cdot AD}{AE}=\frac{900×1700}{1500}$ = 1020(m).
∴B，C，D三厂所建自来水管道的最低造价分别是 720×800 = 576000(元)， 300×800 = 240000(元)， 1020×800 = 816000(元).