《2025年阳光课堂金牌练习册九年级数学下册人教版福建专版》

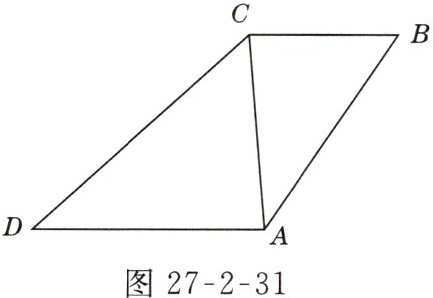
13. 如图27-2-31所示，在四边形ABCD中，∠B = ∠ACD，AB = 6，BC = 4，AC = 5，CD = 7 $\frac{1}{2}$，求AD的长.

答案：

解:
∵ $\frac{AB}{CD}$ =6= 7 $\frac{1}{2}$ $\frac{4}{5}$ , $\frac{BC}{C}$ = $\frac{4}{5}$ ,
∴ $\frac{AB}{CD}$ = $\frac{BC}{C}$ .

又
∵ ∠B=∠ACD,
∴ △ABC∽△DCA,

∴ $\frac{AC}{D}$ = $\frac{AB}{CD}$ ,

即 $\frac{5}{AD}$ = $\frac{4}{5}$  
∴ AD= $\frac{25}{4}$ .

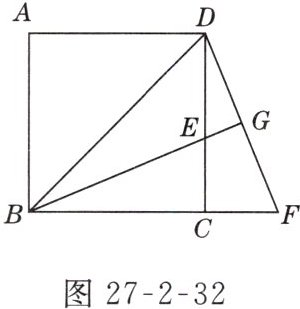
14. 如图27-2-32，已知在正方形ABCD中，BE平分∠DBC，且交CD边于点E，将△BCE绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G.
（1）求证：△BDG∽△DEG；
（2）若EG·BG = 4，求BE的长.

答案：

(1)证明:
∵ BE平分∠DBC,

∴ ∠CBE=∠DBG.

∵ ∠CBE=∠CDF,
∴ ∠DBG=∠CDF;

∵ ∠BGD=∠DGE,
∴ △BDG∽△DEG.

(2)解:
∵ △BDG∽△DEG,
∴ $\frac{DG}{EG}$ = $\frac{BG}{DG}$

∴ DG²=BG.EG=4,
∴ DG=2.

∵ ∠EBC+∠BEC=90°,∠BEC=

∠DEG,∠EBC=∠EDG,

∴ ∠BGD=90°.

∵ ∠DBG=∠FBG,BG=BG,

∴ △BDG≌△BFG.
∴ FG=DG=2,

∴ DF=4.

∵ BE=DF,
∴ BE=DF=4.

1. 相似三角形的对应角__________，对应边________.

答案： 相等@@成比例

2. 三边________的两个三角形相似.

答案： 成比例

3. 两边成比例且________相等的两个三角形相似.

答案： 夹角

4. ________分别相等的两个三角形相似.

答案： 两角

5. 相似三角形__________、__________、________________都等于相似比

答案： 对应高的比@@对应中线的比@@对应角平分线的比

6. 相似三角形面积的比等于__________.

答案： 相似比的平方

7. 根据预习内容，回答问题.
若△ABC∽△A'B'C'，相似比为1∶2，则△ABC与△A'B'C'的面积的比为（ ）
A. 1∶2
B. 2∶1
C. 1∶4
D. 4∶1

答案： C 解析：根据相似三角形的面积比等于相似比的平方的性质直接得出结果：△ABC与△A'B'C'的面积的比为1：4.