第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 [2025昆明东川区期末]下列方程中,是一元二次方程的是 ( )
A.$x^{2}= x+1$
B.$y^{2}+x= 1$
C.$2x+1= 0$
D.$x+\frac{1}{x}= 1$
A.$x^{2}= x+1$
B.$y^{2}+x= 1$
C.$2x+1= 0$
D.$x+\frac{1}{x}= 1$
答案:
A 知识点拨:一元二次方程需要满足的三个条件:①是整式方程;②整理后的方程只含有一个未知数;③整理后的方程未知数的最高次数是2.B项,含有2个未知数;C项,未知数的最高次数是1;D项,$\frac{1}{x}$是分式,不是整式.只有A项符合题意.
2 若方程$kx^{2}+x= 2x^{2}+1$是关于x的一元二次方程,则k的取值范围是____.
答案:
k≠2 移项,得$kx^{2}-2x^{2}+x-1=0$,即$(k-2)x^{2}+x-1=0$,由题意,得$k-2≠0$(二次项系数不为0),解得$k≠2$.
3 易错题[2024宿州埇桥区期中]已知方程$(m-2)x^{|m|}-bx-1= 0$是关于x的一元二次方程,则m的值为____.
答案:
-2

易错分析
本题在求解时,容易忽略二次项系数不为0这一前提条件,导致错误.
-2

易错分析
本题在求解时,容易忽略二次项系数不为0这一前提条件,导致错误.
4 教材P3例题变式[2025成都七中月考]把一元二次方程$(x+1)(x-1)= 3x$化成一般形式,正确的是 ( )
A.$x^{2}-3x-1= 0$
B.$x^{2}-3x+1= 0$
C.$x^{2}+3x-1= 0$
D.$x^{2}+3x+1= 0$
A.$x^{2}-3x-1= 0$
B.$x^{2}-3x+1= 0$
C.$x^{2}+3x-1= 0$
D.$x^{2}+3x+1= 0$
答案:
A $(x+1)(x-1)=3x$,去括号,得$x^{2}-1=3x$.移项,得$x^{2}-3x-1=0$(移项要变号).
5 教材P4练习T1变式 将一元二次方程$\frac{1}{3}x(x-2)= 5$化为二次项系数为1的一般形式是____,其中一次项是____,常数项是____.
答案:
$x^{2}-2x-15=0$ -2x -15 由$\frac{1}{3}x(x-2)=5$,得$\frac{1}{3}x^{2}-\frac{2}{3}x-5=0$,将二次项系数化为1,得$x^{2}-2x-15=0$,所以一次项是-2x,常数项是-15.
6 教材P4T3变式[2025漳州长泰区期中]若一元二次方程有一个根是$x= 1$,则这个方程可以是 ( )
A.$(x+1)(x+2)= 0$
B.$x^{2}-1= 0$
C.$x^{2}-2x-1= 0$
D.$x^{2}+x= 0$
A.$(x+1)(x+2)= 0$
B.$x^{2}-1= 0$
C.$x^{2}-2x-1= 0$
D.$x^{2}+x= 0$
答案:
B 将$x=1$分别代入各选项的方程中,能使方程左右两边相等的即满足题意.
7 教材P4T7变式[2024深圳中考]一元二次方程$x^{2}-3x+a= 0的一个解为x= 1$,则$a= $____.
答案:
2
∵关于x的一元二次方程$x^{2}-3x+a=0$的一个解为$x=1$(x=1满足一元二次方程$x^{2}-3x+a=0$),
∴$1-3+a=0$,解得$a=2$.
∵关于x的一元二次方程$x^{2}-3x+a=0$的一个解为$x=1$(x=1满足一元二次方程$x^{2}-3x+a=0$),
∴$1-3+a=0$,解得$a=2$.
8 [2024南充中考]已知m是方程$x^{2}+4x-1= 0$的一个根,则$(m+5)(m-1)$的值为____.
答案:
-4
∵m是方程$x^{2}+4x-1=0$的一个根,
∴$m^{2}+4m=1$,
∴$(m+5)(m-1)=m^{2}-m+5m-5=m^{2}+4m-5=1-5=-4$.
∵m是方程$x^{2}+4x-1=0$的一个根,
∴$m^{2}+4m=1$,
∴$(m+5)(m-1)=m^{2}-m+5m-5=m^{2}+4m-5=1-5=-4$.
9 教材P4T6变式[2025武汉蔡甸区月考]九年级(5)班文学小组在图书共享仪式上互赠图书,每个同学都把自己的图书给本组其他成员赠送一本,全组共送了132本图书.若设全组共有x名同学,则可列方程为 ( )
A.$x(x-1)= 132$
B.$x(x+1)= 132$
C.$\frac{1}{2}x(x-1)= 132$
D.$\frac{1}{2}x(x+1)= 132$
A.$x(x-1)= 132$
B.$x(x+1)= 132$
C.$\frac{1}{2}x(x-1)= 132$
D.$\frac{1}{2}x(x+1)= 132$
答案:
A 因为全组共有x名同学,所以每个同学需送出(x-1)本图书,所以可列方程为$x(x-1)=132$.
10 新趋势·数学文化[2025太原小店区多校月考]《九章算术》是我国传统数学中重要的著作之一,其中记载:“今有户高多于广六尺八寸,两隅相去适一丈,问户高、广各几何?”大意:有一形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,问它的高与宽各是多少?设矩形门宽为x尺,则依题意所列方程为(1丈= 10尺,1尺= 10寸) ( )
A.$x^{2}+(x+6.8)^{2}= 10^{2}$
B.$x^{2}+(x-6.8)^{2}= 10^{2}$
C.$x(x+6.8)= 10^{2}$
D.$x(x-6.8)= 10^{2}$
A.$x^{2}+(x+6.8)^{2}= 10^{2}$
B.$x^{2}+(x-6.8)^{2}= 10^{2}$
C.$x(x+6.8)= 10^{2}$
D.$x(x-6.8)= 10^{2}$
答案:
A
∵矩形门的高比宽多6尺8寸,且门宽为x尺,
∴门高为$(x+6.8)$尺.根据题意,得$x^{2}+(x+6.8)^{2}=10^{2}$.
∵矩形门的高比宽多6尺8寸,且门宽为x尺,
∴门高为$(x+6.8)$尺.根据题意,得$x^{2}+(x+6.8)^{2}=10^{2}$.
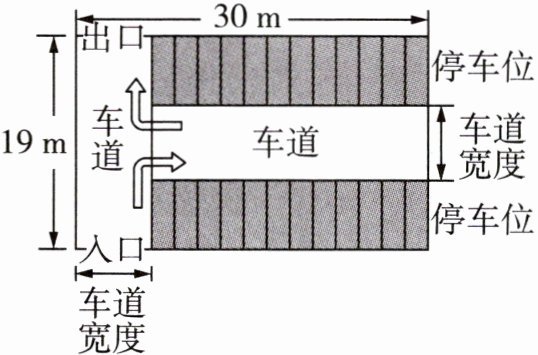
11 新情境[2025咸阳秦都中学期中]如图是某停车场的平面示意图,停车场外围的长为30m,宽为19m.停车场内车道的宽都相等,若停车位的总占地面积为$390m^{2}$,列方程求解车道宽度时,设车道宽度为xm,下列方程正确的是 ( )
A.$19x+30x= 30×19-390$
B.$2x^{2}+30x= 30×19-390$
C.$(30-x)(19-2x)= 390$
D.$(30-x)(19-x)= 390$

A.$19x+30x= 30×19-390$
B.$2x^{2}+30x= 30×19-390$
C.$(30-x)(19-2x)= 390$
D.$(30-x)(19-x)= 390$
答案:
D
查看更多完整答案,请扫码查看


