2025年高考领航高中同步测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高考领航高中同步测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
1. 在等比数列$\{ a_{n}\}$中,若$a_{2}a_{4}a_{6}a_{8}=16$,则$a_{5}=$ (
A.$-2$
B.$3$
C.$-2$或$2$
D.$4$
C
)A.$-2$
B.$3$
C.$-2$或$2$
D.$4$
答案:
C 由等比数列的性质得$a_{2}a_{4}a_{6}a_{8}=a_{5}^{4}=16$,可得$a_{5}=\pm2$.故选C.
2. 在等比数列$\{ a_{n}\}$中,$a_{1}=\frac {1}{8}$,$q = 2$,则$a_{4}$与$a_{8}$的等比中项是 (
A.$\pm 4$
B.$4$
C.$\pm \frac {1}{4}$
D.$\frac {1}{4}$
B
)A.$\pm 4$
B.$4$
C.$\pm \frac {1}{4}$
D.$\frac {1}{4}$
答案:
B 由题意,得$a_{4}=a_{1}q^{3}=\frac{1}{8}×2^{3}=1$,$a_{8}=a_{1}q^{7}=\frac{1}{8}×2^{7}=16$,所以$a_{4}$与$a_{8}$的等比中项为$a_{6}=4$.
3. 某工厂去年产值为$a$,计划$10$年内每年比上一年产值增长$10\%$,那么从今年起第几年这个工厂的产值将超过$2a$ (
A.$6$
B.$7$
C.$8$
D.$9$
C
)A.$6$
B.$7$
C.$8$
D.$9$
答案:
C 设从今年起第$n$年这个工厂的产值为$a_{n}$,则$a_{1}=1.1a,a_{2}=1.1^{2}a,·s,a_{n}=1.1^{n}a$.依题意,得$1.1^{n}a>2a$,即$1.1^{n}>2$,解得$n\geqslant8$.
4. 拓扑结构图是指由网络节点设备和通信介质构成的网络结构图.某树形拓扑结构图如图所示,圆圈代表节点,每一个节点都有两个子节点,则第$10$层节点的个数为 (
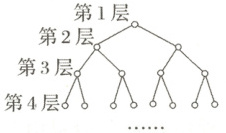
A.$100$
B.$128$
C.$512$
D.$1024$
C
)
A.$100$
B.$128$
C.$512$
D.$1024$
答案:
C 由题图可知,每一层的节点数组成以$1$为首项,$2$为公比的等比数列,所以第$10$层节点的个数是$a_{10}=1×2^{10-1}=512$.
5. 在各项均为正数的等比数列$\{ a_{n}\}$中,$a_{2}=4$,$a_{6}=64$,前$n$项和$S_{n}=510$,则$n=$ (
A.$6$
B.$7$
C.$8$
D.$9$
C
)A.$6$
B.$7$
C.$8$
D.$9$
答案:
C 由题意知$q^{4}=\frac{a_{6}}{a_{2}}=16$且$q>0$,则$q=2,a_{1}=2$,$\therefore S_{n}=\frac{2(1-2^{n})}{1-2}=510$,解得$n=8$.
6. 在等比数列$\{ a_{n}\}$中,$a_{4}=3a_{3}$,则$\frac {a_{2}}{a_{1}}+\frac {a_{4}}{a_{2}}+\frac {a_{6}}{a_{3}}+·s +\frac {a_{2n}}{a_{n}}=$ (
A.$\frac {3^{-n}-3}{2}$
B.$\frac {3^{1 - n}-3}{2}$
C.$\frac {3^{n}-3}{2}$
D.$\frac {3^{n + 1}-3}{2}$
D
)A.$\frac {3^{-n}-3}{2}$
B.$\frac {3^{1 - n}-3}{2}$
C.$\frac {3^{n}-3}{2}$
D.$\frac {3^{n + 1}-3}{2}$
答案:
D 设等比数列$\{a_{n}\}$的公比为$q$.$\because a_{4}=3a_{3},\therefore q=3$.$\therefore\frac{a_{2}+a_{4}+a_{6}+·s+a_{2n}}{a_{1}+a_{2}+a_{3}+·s+a_{n}}=\frac{q+q^{2}+q^{3}+·s+q^{n}}{a_{n}}$ $=\frac{q(1-q^{n})}{1-q}=\frac{3×(1-3^{n})}{1-3}=\frac{3^{n+1}-3}{2}$
7. 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯.”意思是:一座七层塔共挂了$381$盏灯,且相邻两层中的下一层灯数是上一层灯数的$2$倍,则塔的顶层共有灯 (
A.$2$盏
B.$3$盏
C.$5$盏
D.$6$盏
B
)A.$2$盏
B.$3$盏
C.$5$盏
D.$6$盏
答案:
B 设第七层有$a$盏灯,由题意知第七层至第一层的灯的盏数构成一个以$a$为首项,以$2$为公比的等比数列,由等比数列的求和公式可得$a(1-2^{7}){1-2}=381$,解得$a=3$,故顶层有$3$盏灯.
8. 已知数列$\{ a_{n}\}$是公差$d$不为$0$的等差数列,且$a_{1}$,$a_{3}$,$a_{7}$为等比数列$\{ b_{n}\}$的连续三项,则$\frac {b_{3}+b_{4}}{b_{4}+b_{5}}$的值为 (
A.$\frac {1}{2}$
B.$4$
C.$2$
D.$\sqrt {2}$
A
)A.$\frac {1}{2}$
B.$4$
C.$2$
D.$\sqrt {2}$
答案:
A 由题意得$a_{3}^{2}=a_{1}a_{7}$,可得$(a_{1}+2d)^{2}=a_{1}(a_{1}+6d)$,即$a_{1}=2d\neq0$.设数列$\{b_{n}\}$的公比为$q$,则$q=\frac{a_{3}}{a_{1}}=\frac{a_{1}+2d}{a_{1}}=\frac{4d}{2d}=2$,则$\frac{b_{3}+b_{4}}{b_{4}+b_{5}}=\frac{b_{3}(1+q)}{b_{4}(1+q)}=\frac{1}{q}=\frac{1}{2}$.
9. 设等比数列$\{ a_{n}\}$的公比为$q$,则有 (
A.数列$\{ a_{n}a_{n + 1}\}$是公比为$q^{2}$的等比数列
B.数列$\{ a_{n}+a_{n + 1}\}$是公比为$q$的等比数列
C.数列$\{ a_{n}-a_{n + 1}\}$是公比为$q$的等比数列
D.数列$\{\frac {1}{a_{n}}\}$是公比为$\frac {1}{q}$的等比数列
AD
)A.数列$\{ a_{n}a_{n + 1}\}$是公比为$q^{2}$的等比数列
B.数列$\{ a_{n}+a_{n + 1}\}$是公比为$q$的等比数列
C.数列$\{ a_{n}-a_{n + 1}\}$是公比为$q$的等比数列
D.数列$\{\frac {1}{a_{n}}\}$是公比为$\frac {1}{q}$的等比数列
答案:
AD 对于A.由$\frac{a_{n}a_{n+1}}{a_{n-1}a_{n}}=q^{2}(n\geqslant2)$知其公比为$q^{2}$的等比数列,A正确;对于B.若$q=-1$时,$\{a_{n}+a_{n+1}\}$项中有$0$,不是等比数列,B错误;对于C.若$q=1$时,数列$\{a_{n}-a_{n+1}\}$项中有$0$,不是等比数列,C错误;对于D.$\frac{\frac{1}{a_{n+1}}}{\frac{1}{a_{n}}}=\frac{a_{n}}{a_{n+1}}=\frac{1}{q}$,所以数列$\{\frac{1}{a_{n}}\}$是公比为$\frac{1}{q}$的等比数列,D正确.
查看更多完整答案,请扫码查看


