《2025年高考领航高中同步测试卷高中数学选择性必修第二册人教版》

1. 若函数$y=ax+b$在区间$[1,2]$上的平均变化率为 3$,$则实数$a=$
(C)

A.$-3$
B.$2$
C.$3$
D.$-2$

答案： 1.C 根据平均变化率的定义，可知$\frac{\Delta y}{\Delta x}=\frac{(2a+b)-(a+b)}{2-1}=a=3$.故选C.

2. 函数$f(x)=x+2$在$x=3$处的瞬时变化率等于
(A)

A.$1$
B.$2$
C.$3$
D.$4$

答案： 2.A 由$f(x)=x+2$，得$f^{\prime}(3)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0}\frac{3+\Delta x+2-5}{\Delta x}=1$.

3. 做匀变速直线运动的物体的位移为$s(t)=t^{2}+2t(t$的单位:s$,s$的单位:m$),$则物体在$2$ s时的瞬间速度等于
(D)

A.$3$ m/s
B.$4$ m/s
C.$5$ m/s
D.$6$ m/s

答案： 3.D 因为$\Delta s=s(2+\Delta t)-s(2)$，所以$\Delta s=[(2+\Delta t)^{2}+2(2+\Delta t)]-(2^{2}+2×2)=6\Delta t+(\Delta t)^{2}$.
所以$\frac{\Delta s}{\Delta t}=6+\Delta t$.当$\Delta t$趋近于0时，$\frac{\Delta s}{\Delta t}$趋近于6.
所以物体在2s时的瞬时速度为6m/s.

4. 若曲线y=f(x)在其上一点(1,3)处的切线过点(0,2),则
(A)
$A.f^{\prime}(1)＞0 B.f^{\prime}(1)=0 C.f^{\prime}(1)＜0 D.f^{\prime}(1)$不存在

答案： 4.A 由题意知切线过点(1,3)，(0,2)，所以切线的斜率$k=f^{\prime}(1)=\frac{3-2}{1-0}=1＞0$.

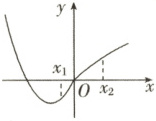
5. 已知函数$f(x)$的图象如图所示$,f^{\prime}(x)$为$f(x)$的导函数$,$根据图象判断下列叙述正确的是
(B)


A.$f^{\prime}(x_{1})＜f^{\prime}(x_{2})$
B.$f^{\prime}(x_{1})＞f^{\prime}(x_{2})$
C.$f(x_{1})＜f^{\prime}(x_{2})＜0$
D.$f(x_{1})＞f^{\prime}(x_{2})＞0$

答案： 5.B 由曲线上一点的导数表示该点切线的斜率，并结合图象知$f^{\prime}(x_{1})＞f^{\prime}(x_{2})＞0$，故选B.

6. 已知曲线$f(x)=\frac{1}{2}x^{2}+x$的一条切线的斜率是 3$,$则切点的横坐标为
(D)

A.$-2$
B.$-1$
C.$1$
D.$2$

答案： 6.D $\because \Delta y=f(x+\Delta x)-f(x)=\frac{1}{2}(x+\Delta x)^{2}+(x+\Delta x)-\frac{1}{2}x^{2}-x=x·\Delta x+\frac{1}{2}(\Delta x)^{2}+\Delta x$，
$\therefore \frac{\Delta y}{\Delta x}=x+\frac{1}{2}\Delta x+1$，
$\therefore f^{\prime}(x)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=x+1$.
设切点坐标为$(x_{0},y_{0})$，则$f^{\prime}(x_{0})=x_{0}+1=3$，
$\therefore x_{0}=2$，故选D.

7. $\lim_{\Delta x \longrightarrow 0}\frac{(1 + \Delta x)^{2} - 1}{\Delta x}$表示
(B)

A.曲线$y = x^{2}$切线的斜率
B.曲线$y = x^{2}$在点$(1,1)$处切线的斜率
C.曲线$y = - x^{2}$切线的斜率
D.曲线$y = - x^{2}$在点$(1, - 1)$处切线的斜率

答案： 7.B 当$y=f(x)=x^{2}$时，$\lim_{\Delta x \to 0}\frac{(1+\Delta x)^{2}-1}{\Delta x}=\lim_{\Delta x \to 0}\frac{f(1+\Delta x)-f(1)}{\Delta x}$，可知$\lim_{\Delta x \to 0}\frac{(1+\Delta x)^{2}-1}{\Delta x}$表示$y=f(x)=x^{2}$在点(1,1)处的切线的斜率.故选B.

8. 设函数$y = f(x)$在$\mathbf{R}$上可导$,$则$\lim_{\Delta x \longrightarrow 0}\frac{f(1 + \Delta x) - f(1)}{3\Delta x}$等于
(C)

A.$f^{\prime}(1)$
B.$3f^{\prime}(1)$
C.$\frac{1}{3}f^{\prime}(1)$
D.以上都不对

答案： 8.C 根据导数的定义
$\lim_{\Delta x \to 0}\frac{f(1+\Delta x)-f(1)}{\Delta x}=f^{\prime}(1)$.
所以$\lim_{\Delta x \to 0}\frac{f(1+\Delta x)-f(1)}{3\Delta x}=\frac{1}{3}\lim_{\Delta x \to 0}\frac{f(1+\Delta x)-f(1)}{\Delta x}=\frac{1}{3}f^{\prime}(1)$，故选C.

9. 物体自由落体运动的方程为$s = s(t) = \frac{1}{2}gt^{2}(g = 9.8 m/s^{2})$.若$v = \lim_{\Delta t \longrightarrow 0}\frac{s(1 + \Delta t) - s(1)}{\Delta t} = 9.8 m/s$,那么说法正确的是
(BC)

A.$\frac{s(1 + \Delta t) - s(1)}{\Delta t}$是物体在$t = 1$ s这一时刻的速率
B.$\frac{s(1 + \Delta t) - s(1)}{\Delta t}$是物体在$1$ s到$(1 + \Delta t)$s这段时间内的平均速率
C.$9.8$ m/s是物体在$t = 1$ s这一时刻的速率
D.$9.8$ m/s是物体在$1$ s到$(1 + \Delta t)$s这段时间内的平均速率

答案： 9.BC 由$\frac{s(1+\Delta t)-s(1)}{\Delta t}$与$\lim_{\Delta t \to 0}\frac{s(1+\Delta t)-s(1)}{\Delta t}$的几何意义可知，$\frac{s(1+\Delta t)-s(1)}{\Delta t}$是物体在1s到$(1+\Delta t)$s这段时间内的平均速率，
$\lim_{\Delta t \to 0}\frac{s(1+\Delta t)-s(1)}{\Delta t}$是在$t=1s$时的瞬时速率.