2025年高考领航高中同步测试卷高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高考领航高中同步测试卷高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
11. 已知函数 $f(x)$ 与 $f'(x)$ 的图象如图所示,则下列结论正确的为 (
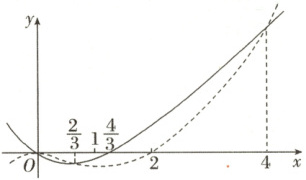
A.实线是 $f(x)$ 的图象,虚线是 $f'(x)$ 的图象
B.实线是 $f'(x)$ 的图象,虚线是 $f(x)$ 的图象
C.不等式组 $\begin{cases}f(x)>f'(x)\\0<x<4\end{cases}$ 的解集为 $(0,\frac{2}{3})$
D.不等式组 $\begin{cases}f(x)>f'(x)\\0<x<4\end{cases}$ 的解集为 $(1,\frac{4}{3})$
BC
)
A.实线是 $f(x)$ 的图象,虚线是 $f'(x)$ 的图象
B.实线是 $f'(x)$ 的图象,虚线是 $f(x)$ 的图象
C.不等式组 $\begin{cases}f(x)>f'(x)\\0<x<4\end{cases}$ 的解集为 $(0,\frac{2}{3})$
D.不等式组 $\begin{cases}f(x)>f'(x)\\0<x<4\end{cases}$ 的解集为 $(1,\frac{4}{3})$
答案:
11.BC 结合图象,若虚线是$f^{\prime}(x)$的图象,则当$x \in (0,2)$时,$f^{\prime}(x) < 0$,则$f(x)$在$(0,2)$上单调递减,与实线中$f(x)$在$(0,2)$上不单调矛盾,不满足题意,故实线为$f^{\prime}(x)$的图象,虚线为$f(x)$的图象,故A不正确,B正确;由图象知不等式组$\begin{cases} f(x) > f^{\prime}(x) \\0 < x < 4 \end{cases}$的解集为$(0,\frac{2}{3})$,故C正确,D不正确. 故选BC.
12. 函数 $f(x)=\ln x - \frac{x}{1 + 2x}$ 在定义域内为
增
函数(填“增”或“减”).
答案:
12.解析:由已知得$f(x)$的定义域为$(0, +\infty)$.
$\because f(x) = \ln x - \frac{x}{1 + 2x}$,
$\therefore f^{\prime}(x) = \frac{1}{x} - \frac{1 + 2x - 2x}{(1 + 2x)^{2}} = \frac{4x^{2} + 3x + 1}{x(1 + 2x)^{2}}$.
$\because x > 0$,$\therefore 4x^{2} + 3x + 1 > 0,x(1 + 2x)^{2} > 0$.
$\therefore$当$x > 0$时,$f^{\prime}(x) > 0$. $\therefore f(x)$在$(0, +\infty)$内为增函数.
答案:增
$\because f(x) = \ln x - \frac{x}{1 + 2x}$,
$\therefore f^{\prime}(x) = \frac{1}{x} - \frac{1 + 2x - 2x}{(1 + 2x)^{2}} = \frac{4x^{2} + 3x + 1}{x(1 + 2x)^{2}}$.
$\because x > 0$,$\therefore 4x^{2} + 3x + 1 > 0,x(1 + 2x)^{2} > 0$.
$\therefore$当$x > 0$时,$f^{\prime}(x) > 0$. $\therefore f(x)$在$(0, +\infty)$内为增函数.
答案:增
13. 若 $y = x + \frac{a^2}{x}(a>0)$ 在 $[2,+\infty)$ 上是增函数,则 $a$ 的取值范围是
(0,2]
.
答案:
13.解析:由$y^{\prime} = 1 - \frac{a^{2}}{x^{2}} \geq 0$,得$x \leq -a$或$x \geq a$.
$\therefore y = x + \frac{a^{2}}{x}$的单调递增区间为$(-\infty, -a]$,$[a, +\infty)$.
$\because$函数在$[2, +\infty)$上单调递增,
$\therefore [2, +\infty) \subseteq [a, +\infty)$,$\therefore a \leq 2$.
又$a > 0$,$\therefore 0 < a \leq 2$.
答案:$(0,2]$
$\therefore y = x + \frac{a^{2}}{x}$的单调递增区间为$(-\infty, -a]$,$[a, +\infty)$.
$\because$函数在$[2, +\infty)$上单调递增,
$\therefore [2, +\infty) \subseteq [a, +\infty)$,$\therefore a \leq 2$.
又$a > 0$,$\therefore 0 < a \leq 2$.
答案:$(0,2]$
14. 已知函数 $y = f(x)(x\in\mathbf{R})$ 的图象如图所示,则不等式 $xf'(x)\geqslant0$ 的解集为
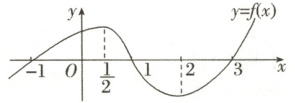
[0,\frac{1}{2}] \cup [2, +\infty)
.
答案:
14.解析:由$f(x)$图象特征可得,在$(-\infty,\frac{1}{2}]$和$[2, +\infty)$上$f^{\prime}(x) \geq 0$,在$(\frac{1}{2},2)$上$f^{\prime}(x) < 0$,
所以$xf^{\prime}(x) \geq 0 \Leftrightarrow \begin{cases} x \geq 0, \\ f^{\prime}(x) \geq 0 \end{cases}$或$\begin{cases} x \leq 0, \\ f^{\prime}(x) \leq 0 \end{cases} \Leftrightarrow$
$0 \leq x \leq \frac{1}{2}$或$x \geq 2$,所以$xf^{\prime}(x) \geq 0$的解集为$[0,\frac{1}{2}] \cup [2, +\infty)$.
答案:$[0,\frac{1}{2}] \cup [2, +\infty)$
所以$xf^{\prime}(x) \geq 0 \Leftrightarrow \begin{cases} x \geq 0, \\ f^{\prime}(x) \geq 0 \end{cases}$或$\begin{cases} x \leq 0, \\ f^{\prime}(x) \leq 0 \end{cases} \Leftrightarrow$
$0 \leq x \leq \frac{1}{2}$或$x \geq 2$,所以$xf^{\prime}(x) \geq 0$的解集为$[0,\frac{1}{2}] \cup [2, +\infty)$.
答案:$[0,\frac{1}{2}] \cup [2, +\infty)$
15. (13 分)求下列函数的单调区间.
(1) $f(x)=x^2· e^{-x}$;
(2) $f(x)=x + \frac{1}{x}$.
(1) $f(x)=x^2· e^{-x}$;
(2) $f(x)=x + \frac{1}{x}$.
答案:
15.解:
(1)易知函数的定义域为$(-\infty, +\infty)$.
$f^{\prime}(x) = (x^{2})^{\prime}e^{-x} + x^{2}(e^{-x})^{\prime} = 2xe^{-x} - x^{2}e^{-x} = e^{-x} · (2x - x^{2})$,
令$f^{\prime}(x) = 0$,得$x = 0$或$x = 2$,
当$x$变化时,$f^{\prime}(x),f(x)$的变化情况如下表:
$x$ $(-\infty,0)$ $0$ $(0,2)$ $2$ $(2,+\infty)$
$f^{\prime}(x)$ $-$ $0$ $+$ $0$ $-$
$f(x)$ 单调递减 $f(0)$ 单调递增 $f(2)$ 单调递减
$\therefore f(x)$的单调递减区间为$(-\infty,0)$和$(2, +\infty)$,单调递增区间为$(0,2)$.
(2)易知函数的定义域为$(-\infty,0) \cup (0, +\infty)$,且$f^{\prime}(x) = 1 - \frac{1}{x^{2}}$,
令$f^{\prime}(x) = 0$,得$x = -1$或$x = 1$,
当$x$变化时,$f^{\prime}(x),f(x)$的变化情况如下表:
$x$ $(-\infty,-1)$ $-1$ $(-1,0)$ $(0,1)$ $1$ $(1,+\infty)$
$f^{\prime}(x)$ $+$ $0$ $-$ $-$ $0$ $+$
$f(x)$ 单调递增 $f(-1)$ 单调递减 单调递减 $f(1)$ 单调递增
$\therefore$函数$f(x)$的单调递减区间为$(-1,0)$和$(0, 1)$,单调递增区间为$(-\infty,-1)$和$(1, +\infty)$.
(1)易知函数的定义域为$(-\infty, +\infty)$.
$f^{\prime}(x) = (x^{2})^{\prime}e^{-x} + x^{2}(e^{-x})^{\prime} = 2xe^{-x} - x^{2}e^{-x} = e^{-x} · (2x - x^{2})$,
令$f^{\prime}(x) = 0$,得$x = 0$或$x = 2$,
当$x$变化时,$f^{\prime}(x),f(x)$的变化情况如下表:
$x$ $(-\infty,0)$ $0$ $(0,2)$ $2$ $(2,+\infty)$
$f^{\prime}(x)$ $-$ $0$ $+$ $0$ $-$
$f(x)$ 单调递减 $f(0)$ 单调递增 $f(2)$ 单调递减
$\therefore f(x)$的单调递减区间为$(-\infty,0)$和$(2, +\infty)$,单调递增区间为$(0,2)$.
(2)易知函数的定义域为$(-\infty,0) \cup (0, +\infty)$,且$f^{\prime}(x) = 1 - \frac{1}{x^{2}}$,
令$f^{\prime}(x) = 0$,得$x = -1$或$x = 1$,
当$x$变化时,$f^{\prime}(x),f(x)$的变化情况如下表:
$x$ $(-\infty,-1)$ $-1$ $(-1,0)$ $(0,1)$ $1$ $(1,+\infty)$
$f^{\prime}(x)$ $+$ $0$ $-$ $-$ $0$ $+$
$f(x)$ 单调递增 $f(-1)$ 单调递减 单调递减 $f(1)$ 单调递增
$\therefore$函数$f(x)$的单调递减区间为$(-1,0)$和$(0, 1)$,单调递增区间为$(-\infty,-1)$和$(1, +\infty)$.
查看更多完整答案,请扫码查看


