《2025年新课程学习与检测八年级数学上册》

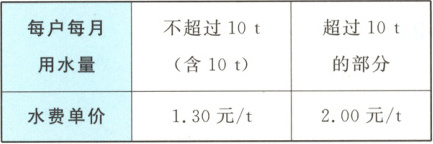
6. 为了鼓励居民节约用水，某地水费按下表规定收取.
(1) 若某户用水量为 $ x $ t，需付水费为 $ y $ 元，求水费 $ y $(元)与用水量 $ x $(t)之间的函数关系式.
(2) 若小华家四月份付水费 17 元，他家四月份用水多少吨？

答案： 6.解：
(1)当$x\leq10$时，$y = 1.3x$；当$x ＞ 10$时，$y = 13 + 2(x - 10)$。
(2)设小华家四月份用水量为$x\ t$。
$\because17 ＞ 1.30×10$，$\therefore$小华家四月份用水量超过$10\ t$。
由题意得$1.3×10 + (x - 10)×2 = 17$，即$2x = 24$，解得$x = 12$。
答：小华家四月份用水$12\ t$。

7. 某公司计划从厂家采购一批档案袋和手账本，已知档案袋 10 元/个，手账本 15 元/本. 经了解，厂家有两种优惠方案：
方案一：购买手账本没有优惠，购买档案袋不超过 20 个时，每个都按 9 折优惠，超过 20 个时，超过部分每个按 7 折优惠.
方案二：档案袋和手账本都按原价的 8 折优惠.
若该公司购买 $ x $($ x ＞ 20 $)个档案袋，10 本手账本.
(1) 请分别求两种方案下该公司购买档案袋和手账本所需的总费用 $ y $(元)与 $ x $(个)之间的函数关系式.
(2) 若该公司决定购买 30 个档案袋，请帮助该公司选择所花总费用较少的一种.
(3) 当该公司购买多少个档案袋时，选择方案一和方案二所需的总费用相同？

答案： 7.解：
(1)方案一：当$0 ＜ x\leq20$时，$y = 10×0.9x + 15×10 = 9x + 150$；当$x ＞ 20$时，$y = 10×0.7×(x - 20) + 10×0.9×20 + 15×10 = 7x + 190$。
综上所述，$y = \begin{cases}9x + 150(0 ＜ x\leq20),\\7x + 190(x ＞ 20).\end{cases}$
方案二：$y = 10×0.8x + 15×0.8×10 = 8x + 120$。
(2)方案一的费用：$7×30 + 190 = 400$(元)。
方案二的费用：$8×30 + 120 = 360$(元)。
$\because400 ＞ 360$，$\therefore$选择方案二所花总费用较少。
(3)令$7x + 190 = 8x + 120$，得$x = 70$。
答：该公司购买$70$个档案袋时，总费用相同。