《2025年新课程学习与检测八年级数学上册》

3. 若 $ y $ 关于 $ x $ 的函数 $ y = x^{m - 3} + 1 $ 是一次函数，则 $ m $ 的值为(D)

A.$ m = 1 $
B.$ m = - 1 $
C.$ m = - 4 $
D.$ m = 4 $

答案： 3.D

4. 某市出租车的收费标准如下表所示.

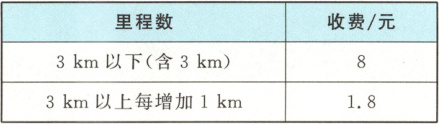
设行驶里程数为 $ x $ km，收费为 $ y $ 元，则 $ y $ 与 $ x(x \geq 3) $ 之间的关系式为(C)

A.$ y = 8x $
B.$ y = 1.8x $
C.$ y = 1.8x + 2.6 $
D.$ y = 1.8x + 8 $

答案： 4.C

5. 若函数 $ y = (m - 2)x^{|m| - 1} + 6 $ 是 $ y $ 关于 $ x $ 的一次函数，则 $ m = $-2.

答案： 5.-2

6. 一根弹簧原长 12 cm，所挂物体的质量每增加 2 kg，弹簧就伸长 6 cm，则悬挂物体后，弹簧长度 $ y $(cm)与所挂物体的质量 $ x $(kg)之间的函数表达式是y=3x+12.

答案： 6.y=3x+12

7. 已知 $ y = (m + 1)x^{2 - |m|} + n + 5 $.
(1)当 $ m,n $ 为何值时，$ y $ 是 $ x $ 的一次函数？
(2)当 $ m,n $ 为何值时，$ y $ 是 $ x $ 的正比例函数？

答案： 7.解：
(1)由条件可知m+1≠0且2-|m|=1，n为任意实数，解得m=1.
(2)由条件可知m+1≠0且2-|m|=1，n+5=0，解得m=1，n=-5.

8. 一位卖报人每天从报社固定购买 100 份报纸，每份进价 0.6 元，然后以每份 1 元的价格出售.报纸卖不完退回报社时，退回的报纸只按进价的 50%退款.如果某一天卖报人卖出的报纸为 $ x $ 份，所获得的利润为 $ y $ 元，试写出 $ y $ 与 $ x $ 的表达式：y=0.7x-30.

答案： 8.y=0.7x-30

9. 已知 $ y + a $ 与 $ x - b $ 成正比例(其中 $ a,b $ 都是常数).
(1)试说明 $ y $ 是 $ x $ 的一次函数.
(2)如果 $ x = - 1 $ 时，$ y = - 15 $，$ x = 7 $ 时，$ y = 1 $，求这个一次函数的解析式.

答案： 9.解：
(1)
∵y+a与x-b成正比例，设比例系数为k，则y+a=k(x-b)，整理得y=kx-kb-a，则y是x的一次函数.
(2)由题意得$\begin{cases} -15=-k-kb-a, \\ 1=7k-kb-a, \end{cases}$解得$\begin{cases} k=2, \\ kb+a=13, \end{cases}$则该一次函数的解析式为y=2x-13.

10. 已知函数 $ y = (m - 1)x + m - 4 $，当 $ m $ 为何值时，函数满足下列要求？
(1)它是一次函数.
(2)它是常值函数.

答案： 10.解：
(1)当m-1≠0，即m≠1时，函数y=(m-1)x+m-4是一次函数.
(2)当m-1=0，即m=1时，函数y=(m-1)x+m-4是常值函数.

11. 一盘蚊香长 105 cm，点燃时每小时缩短 10 cm.
(1)请写出点燃后蚊香的长 $ y $(cm)与蚊香燃烧时间 $ t $(h)之间的函数关系式.
(2)该蚊香可点燃多长时间？

答案： 11.解：
(1)
∵蚊香的长等于蚊香的原长减去燃烧的长度，
∴y=105-10t(0≤t≤10.5).
(2)
∵蚊香燃尽的时候蚊香的长度y=0，
∴105-10t=0，解得t=10.5.
∴该蚊香可点燃10.5h.