《2025年名校课堂八年级数学上册北师大版甘肃专版》

1. 下列函数中,是一次函数,但不是正比例函数的是(D)

A.$ y = -\frac{1}{x} $
B.$ y = x^2 $
C.$ y = x $
D.$ y = \frac{x + 1}{2} $

答案： D

2. 下列曲线中,表示 $ y $ 是 $ x $ 的函数的是(D)

答案： D

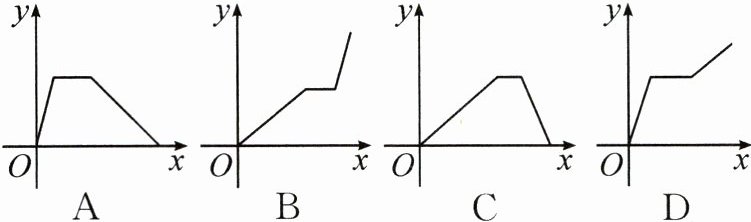
3. 新考向 本地素材 兰州水上巴士 1 号线在黄河上航行,往返于十里店码头和兰州港码头.假设轮船在静水中的速度不变,黄河的水流速度不变.该轮船从兰州港码头出发,逆水航行到十里店码头,停留一段时间,又顺水航行返回兰州港码头.设该轮船从兰州港码头出发后航行的时间为 $ x $,轮船与兰州港码头的距离为 $ y $,则下列各图中,能够反映 $ y $ 与 $ x $ 之间函数关系的大致图象是(C)

答案： C

4. 别让眼泪成为人类的最后一滴水! 为加强节水意识,某市采用如下收费标准:不超过 $ 12 \mathrm{~m}^3 $ 时,按 3 元 $ / \mathrm{m}^3 $ 收费,超过 $ 12 \mathrm{~m}^3 $ 时,超出的部分按 5 元 $ / \mathrm{m}^3 $ 收费.设某用户月用水量为 $ x \mathrm{~m}^3 $,水费为 $ y $ 元.
(1)当 $ x ＞ 12 $ 时,求 $ y $ 关于 $ x $ 的函数表达式.
(2)若该用户某月预算水费 40 元,实际水费 33 元,则该用户本月实际用水比预算少用了多少立方米?

答案：
(1)y=5x−24；
(2)1.8m³

5. (2024·兰州新区期末)已知一次函数 $ y = mx - 2 $, $ y $ 的值随 $ x $ 值的增大而减小,则点 $ P(-m + 1, m) $ 在第四象限.

答案： 四

6. 若一次函数 $ y = (m - 4)x + m^2 - 16 $ 的图象经过原点,则 $ m = $−4.

答案： −4

7. (2024·兰州城关区期末)关于一次函数 $ y = -2x + 3 $,下列结论正确的是(C)

A.图象不经过第二象限
B.图象与 $ x $ 轴的交点是 $ (0, 3) $
C.将一次函数 $ y = -2x + 3 $ 的图象向下平移 3 个单位长度后,所得图象的函数表达式为 $ y = -2x $
D.点 $ (x_1, y_1) $ 和 $ (x_2, y_2) $ 在一次函数 $ y = -2x + 3 $ 的图象上,若 $ x_1 ＜ x_2 $,则 $ y_1 ＜ y_2 $

答案： C

8. (2024·兰州城关区期末)在同一平面直角坐标系中,函数 $ y = kx $ 和 $ y = -kx + k(k \neq 0) $ 的图象可能是(A)

答案： A

9. 如图,$ P $ 是正比例函数 $ y = kx $ 图象上的一点,且点 $ P $ 在第二象限,过点 $ P $ 作 $ PA \perp x $ 轴于点 $ A $.已知 $ OA = 1 $, $ PA = 2 $.
(1)求 $ k $ 的值.
(2)已知点 $ P $ 关于 $ y $ 轴的对称点为点 $ B $,点 $ B $ 关于 $ x $ 轴的对称点为点 $ C $.
①判断点 $ C $ 是否在该正比例函数的图象上,并说明理由.
②计算 $ \triangle APC $ 的面积.

答案：
(1)k=−2；
(2)①点C在该正比例函数的图象上，理由：点C的坐标为(1,−2)，当x=1时，y=−2×1=−2，所以点C在正比例函数y=−2x的图象上；②2