《2025年名校课堂八年级数学上册北师大版甘肃专版》

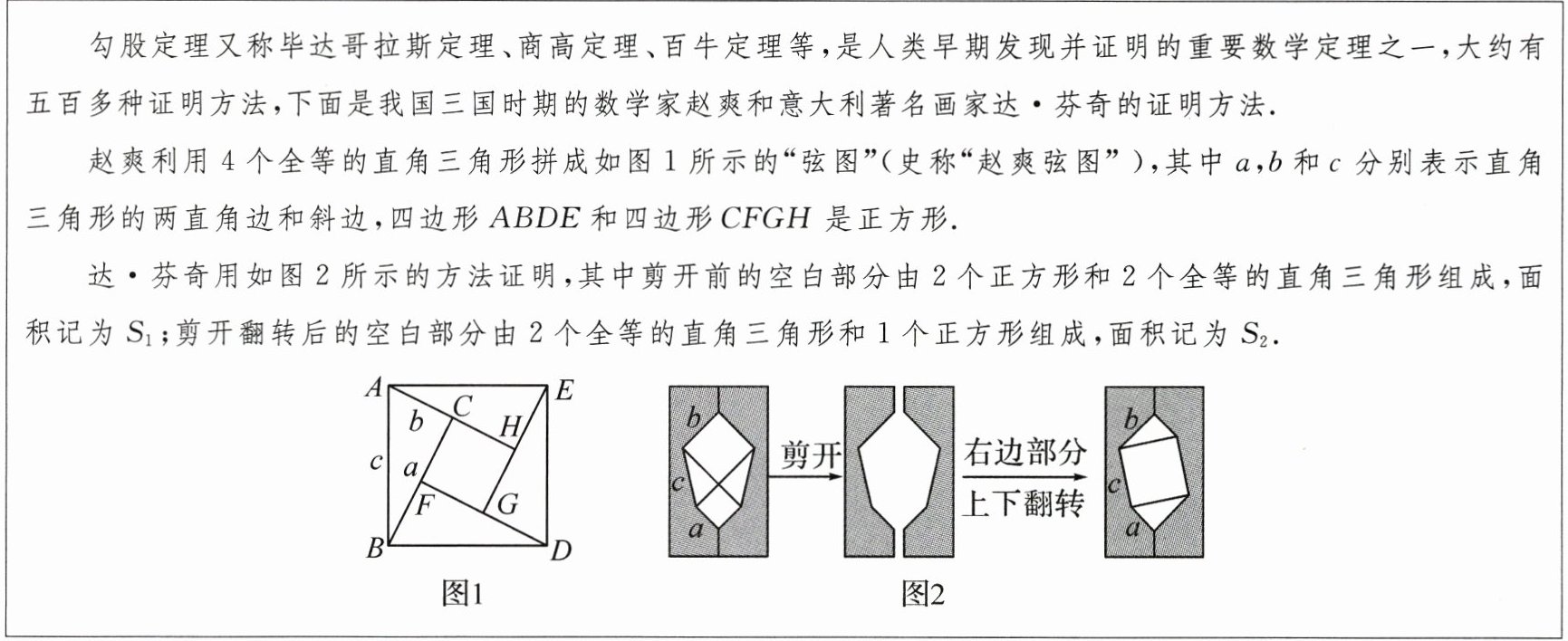
阅读与思考：请阅读下列材料，并完成相应的任务.

任务：
(1)下面是小颖利用赵爽弦图验证勾股定理的过程，请你帮她补充完整.
证明：由图 1，知 $ S_{正方形 ABDE} = 4S_{\triangle ABC} + S_{正方形 CFGH} $，正方形 $ CFGH $ 的边长为 a - b.
$\because S_{正方形 ABDE} = c^{2}$，$ S_{\triangle ABC} = $$\frac{1}{2}$ab，$ S_{正方形 CFGH} = $(a - b)²，
$\therefore c^{2} = 4× \frac{1}{2}ab + (a - b)^{2} = 2ab + a^{2} - 2ab + b^{2} $，即 $ a^{2} + b^{2} = c^{2} $.
(2)请你参照小颖的验证过程，利用图 2 及图中标明的字母写出勾股定理的验证过程.
(3)这种根据图形直观推论或验证数学规律和公式的方法，简称“无字证明”. 实际上，初中数学还有一些代数恒等式(除上述涉及的)也可以借助“无字证明”来直观解释，请你举出一例，画出图形并直接写出所解释的代数恒等式.

答案：

(1)a - b；$\frac{1}{2}$ab；(a - b)²
(2)根据题意，得S₁=a²+b²+2×$\frac{1}{2}$ab=a²+b²+ab，S₂=c²+2×$\frac{1}{2}$ab=c²+ab.
∵ S₁=S₂，
∴ a²+b²+ab=c²+ab，即a²+b²=c².
(3)解：(a + b)²=a²+2ab + b²，图形如图所示．(答案不唯一)