第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
10. 如图,在 $ □ A B C D $ 中,$ M $ 是 $ B C $ 的中点,$ A M = 9 $,$ B D = 12 $,$ A D = 10 $,则四边形 $ A B C D $ 的面积是(
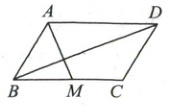
A.30
B.36
C.54
D.72
D
)
A.30
B.36
C.54
D.72
答案:
D
11. 分式 $ \frac { 1 } { 3 x ^ { 2 } y ^ { 2 } } $,$ \frac { 1 } { 4 x y ^ { 3 } } $ 的最简公分母是
$12x^2y^3$
.
答案:
$12x^2y^3$
12. 一个多边形的每一个外角都等于 $ 30 ^ { \circ } $,则这个多边形的边数是
12
.
答案:
12
13. 若 $ m ^ { 2 } = n + 2 $,$ n ^ { 2 } = m + 2 ( m \neq n ) $,则 $ m ^ { 3 } - 2 m n + n ^ { 3 } $ 的值为
-2
.
答案:
-2
14. 学校篮球队五名队员的年龄分别为 17,15,17,16,15,其方差为 0.8,则 3 年后这五名队员年龄的方差为
0.8
.
答案:
0.8
15. 如图,在 $ □ A B C D $ 中,$ E $ 为边 $ C D $ 上一点,将 $ \triangle A D E $ 沿 $ A E $ 折叠至 $ \triangle A D ^ { \prime } E $ 处,$ A D ^ { \prime } $ 与 $ C E $ 交于点 $ F $.若 $ \angle B = 50 ^ { \circ } $,$ \angle D A E = 25 ^ { \circ } $,则 $ \angle F E D ^ { \prime } = $
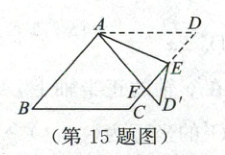
30°
.
答案:
30°
16. 如图,在 $ \triangle A B C $ 中,$ A B = 4 $,$ B C = 6 $,$ \angle B = 60 ^ { \circ } $.将 $ \triangle A B C $ 沿射线 $ B C $ 的方向平移,得到 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $,再将 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 绕点 $ A ^ { \prime } $ 逆时针旋转一定角度后,点 $ B ^ { \prime } $ 恰好与点 $ C $ 重合,则平移的距离为
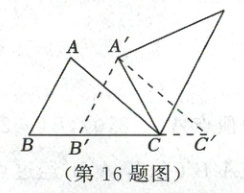
2
.
答案:
$2$
17. (本题 10 分)
因式分解.
(1) $ 3 x ^ { 3 } - 12 x y ^ { 2 } $;
(2) $ n ^ { 2 } ( m - 2 ) + 4 ( 2 - m ) $.
因式分解.
(1) $ 3 x ^ { 3 } - 12 x y ^ { 2 } $;
(2) $ n ^ { 2 } ( m - 2 ) + 4 ( 2 - m ) $.
答案:
(1)
首先,从 $3x^{3} - 12xy^{2}$ 中提取最大公因式 $3x$,得到:
$3x^{3} - 12xy^{2} = 3x(x^{2} - 4y^{2})$
接着,利用平方差公式 $a^{2} - b^{2} = (a + b)(a - b)$,将 $x^{2} - 4y^{2}$ 分解为 $(x + 2y)(x - 2y)$,所以:
$3x(x^{2} - 4y^{2}) = 3x(x + 2y)(x - 2y)$
(2)
首先,从 $n^{2}(m - 2) + 4(2 - m)$ 中变形得到:
$n^{2}(m - 2) - 4(m - 2)$
接着提取公因式 $(m - 2)$,得到:
$(m - 2)(n^{2} - 4)$
再利用平方差公式,将 $n^{2} - 4$ 分解为 $(n + 2)(n - 2)$,所以:
$(m - 2)(n^{2} - 4) = (m - 2)(n + 2)(n - 2)$
(1)
首先,从 $3x^{3} - 12xy^{2}$ 中提取最大公因式 $3x$,得到:
$3x^{3} - 12xy^{2} = 3x(x^{2} - 4y^{2})$
接着,利用平方差公式 $a^{2} - b^{2} = (a + b)(a - b)$,将 $x^{2} - 4y^{2}$ 分解为 $(x + 2y)(x - 2y)$,所以:
$3x(x^{2} - 4y^{2}) = 3x(x + 2y)(x - 2y)$
(2)
首先,从 $n^{2}(m - 2) + 4(2 - m)$ 中变形得到:
$n^{2}(m - 2) - 4(m - 2)$
接着提取公因式 $(m - 2)$,得到:
$(m - 2)(n^{2} - 4)$
再利用平方差公式,将 $n^{2} - 4$ 分解为 $(n + 2)(n - 2)$,所以:
$(m - 2)(n^{2} - 4) = (m - 2)(n + 2)(n - 2)$
查看更多完整答案,请扫码查看


