《2025年同步练习册配套检测卷八年级数学上册鲁教版五四制》

18. (本题8分)
某市为治理污水,需要铺设一段全长为3000m的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划提高25%,结果提前30天完成了这一任务,实际每天铺设多长管道?

答案： 设原计划每天铺设管道$ x $米，则实际每天铺设管道$ (1+25\%)x = 1.25x $米。
根据题意，原计划完成任务时间 - 实际完成任务时间 = 30天，可列方程：
$\frac{3000}{x} - \frac{3000}{1.25x} = 30$
解方程：
左边通分计算：
$\frac{3000 × 1.25 - 3000}{1.25x} = \frac{3750 - 3000}{1.25x} = \frac{750}{1.25x}$
则方程化为：
$\frac{750}{1.25x} = 30$
解得：
$1.25x = \frac{750}{30} = 25 \implies x = 20$
实际每天铺设：$ 1.25x = 1.25 × 20 = 25 $米。
检验：原计划时间$ \frac{3000}{20} = 150 $天，实际时间$ \frac{3000}{25} = 120 $天，$ 150 - 120 = 30 $天，符合题意。
答：实际每天铺设25米管道。

19. (本题6分)
如图,在由边长为1的小正方形组成的$5×6$的网格图中,$\triangle ABC$的三个顶点均在格点上,请按要求解答下列问题:
(1)通过计算判断$\triangle ABC$的形状;
(2)在图中确定一个格点D,连接AD,CD,使四边形ABCD为平行四边形,并求出平行四边形ABCD的面积.

答案：

(1)由网格图可知：
$AB=\sqrt{1^{2} + 2^{2}}=\sqrt{5}$；
$AC=\sqrt{2^{2}+4^{2}}=\sqrt{20} = 2\sqrt{5}$；
$BC=\sqrt{3^{2}+4^{2}}=\sqrt{25}=5$。
因为$AB^{2}+AC^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=5 + 20 = 25$，$BC^{2}=25$，所以$AB^{2}+AC^{2}=BC^{2}$。
所以$\triangle ABC$是直角三角形。
(2)如图，在网格中取格点$D$，连接$AD$，$CD$，则四边形$ABCD$为平行四边形。

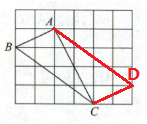
平行四边形$ABCD$的面积$S = BC× AC÷ 2×2$（因为两个全等直角三角形可拼成平行四边形，$\triangle ABC$面积$S_{\triangle ABC}=\frac{1}{2}AC× AB$（这里以$AB$为直角边，在直角三角形中求面积），而平行四边形面积是$\triangle ABC$面积的$2$倍），$AC = 2\sqrt{5}$，$AB=\sqrt{5}$，所以$S= 10$。
综上，（1）$\triangle ABC$是直角三角形；（2）按上述方法确定格点$D$，平行四边形$ABCD$面积为$10$。