《2025年同步练习册配套检测卷八年级数学上册鲁教版五四制》

22. (本题 10 分)
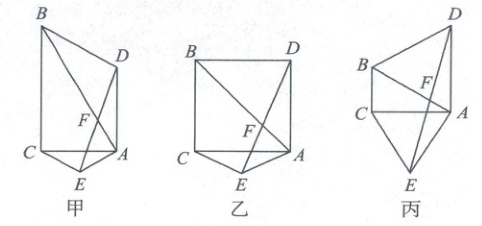
如图甲,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,分别以 $AB$,$AC$ 为底边向$\triangle ABC$ 的外侧作等腰$\triangle ABD$ 和$\triangle ACE$,且 $AD\perp AC$,$AB\perp AE$,$DE$ 和 $AB$ 相交于点 $F$。试探究线段 $FD$,$FE$的数量关系,并加以证明。
说明：如果你经过反复探索,没有找到解决问题的方法,可以从图乙、图丙中选取一个,并分别补充条件$\angle CAB = 45^{\circ}$,$\angle CAB = 30^{\circ}$后,再完成你的证明。

答案： 结论：$FD = FE$
证明：
以点$C$为原点，$AC$所在直线为$x$轴，$BC$所在直线为$y$轴建立平面直角坐标系。设$C(0,0)$，$A(a,0)$，$B(0,b)$（$a＞0,b＞0$）。
1. 求点$E$的坐标
等腰$\triangle ACE$以$AC$为底边，故$E$在$AC$的垂直平分线上，设$E\left(\frac{a}{2},k\right)$。
$AB \perp AE$：
$AB$的斜率$k_{AB} = \frac{b-0}{0-a} = -\frac{b}{a}$，$AE$的斜率$k_{AE} = \frac{k-0}{\frac{a}{2}-a} = -\frac{2k}{a}$。
由$AB \perp AE$，得$k_{AB} \cdot k_{AE} = -1$，即$\left(-\frac{b}{a}\right)\left(-\frac{2k}{a}\right) = -1$，解得$k = -\frac{a^2}{2b}$。
故$E\left(\frac{a}{2}, -\frac{a^2}{2b}\right)$。
2. 求点$D$的坐标
等腰$\triangle ABD$以$AB$为底边，$AB$的中点为$\left(\frac{a}{2},\frac{b}{2}\right)$，$AB$的斜率为$-\frac{b}{a}$，故$AB$的垂直平分线斜率为$\frac{a}{b}$，方程为：
$y - \frac{b}{2} = \frac{a}{b}\left(x - \frac{a}{2}\right)$。
$AD \perp AC$：$AC$为$x$轴，$AD$垂直于$AC$，故$AD$为竖直线$x = a$。
将$x = a$代入$AB$的垂直平分线方程，得：
$y - \frac{b}{2} = \frac{a}{b}\left(a - \frac{a}{2}\right) = \frac{a^2}{2b}$，解得$y = \frac{b}{2} + \frac{a^2}{2b} = \frac{a^2 + b^2}{2b}$。
故$D\left(a, \frac{a^2 + b^2}{2b}\right)$。
3. 证明$F$为$DE$中点
$DE$的中点坐标：
横坐标：$\frac{a + \frac{a}{2}}{2} = \frac{3a}{4}$，纵坐标：$\frac{\frac{a^2 + b^2}{2b} + \left(-\frac{a^2}{2b}\right)}{2} = \frac{b}{4}$，即中点为$\left(\frac{3a}{4}, \frac{b}{4}\right)$。
$AB$的方程：由$A(a,0)$，$B(0,b)$得$\frac{x}{a} + \frac{y}{b} = 1$。
将$\left(\frac{3a}{4}, \frac{b}{4}\right)$代入$AB$方程：$\frac{\frac{3a}{4}}{a} + \frac{\frac{b}{4}}{b} = \frac{3}{4} + \frac{1}{4} = 1$，故中点在$AB$上，即$DE$的中点为$F$。
因此，$F$为$DE$中点，即$FD = FE$。
证毕。