《2025年同步练习册配套检测卷八年级数学上册鲁教版五四制》

17. (本题10分)
(1)计算：$\frac{2x}{5x - 3}÷\frac{3}{25x^{2}-9}\cdot\frac{x}{5x + 3}$。
(2)解方程：$\frac{x + 1}{x}+\frac{1}{x - 2}= 1$。

答案：
(1)
$\begin{aligned}&\frac{2x}{5x - 3}÷\frac{3}{25x^{2}-9}\cdot\frac{x}{5x + 3}\\=&\frac{2x}{5x - 3}\cdot\frac{(5x - 3)(5x + 3)}{3}\cdot\frac{x}{5x + 3}\\=&\frac{2x\cdot(5x - 3)(5x + 3)\cdot x}{(5x - 3)\cdot3\cdot(5x + 3)}\\=&\frac{2x^{2}}{3}\end{aligned}$
(2)
$\begin{aligned}\frac{x + 1}{x}+\frac{1}{x - 2}&= 1\\(x + 1)(x - 2) + x &= x(x - 2)\\x^{2}-2x + x - 2 + x &= x^{2}-2x\\x^{2}-2 &= x^{2}-2x\\-2 &= -2x\\x &= 1\end{aligned}$
检验：当$x = 1$时，$x(x - 2)=1×(1 - 2)= -1≠0$，所以$x = 1$是原方程的解。

18. (本题8分)
如图,在平面直角坐标系$xOy$中,$\triangle ABC三个顶点的坐标分别为A(-5,1)$,$B(-4,4)$,$C(-1,-1)$。将$\triangle ABC$向右平移5个单位长度,再向下平移4个单位长度,得到$\triangle A'B'C'$,其中点$A'$,$B'$,$C'分别为点A$,$B$,$C$的对应点。
(1)请在所给坐标系中画出$\triangle A'B'C'$,并直接写出点$C'$的坐标；
(2)若$AB边上一点P经过上述平移后的对应点为P'(x,y)$,用含$x$,$y的式子表示点P$的坐标；(直接写出结果即可)
(3)求$\triangle A'B'C'$的面积。

答案：

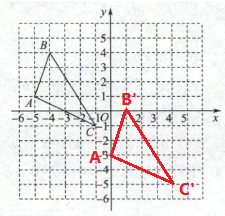
(1) 点$C'$的坐标为$(4,-5)$。
(2) 点$P$的坐标为$(x-5,y+4)$。
(3) $\triangle A'B'C'$的面积为$7$。