《2025年同步练习册北京师范大学出版社六年级数学上册鲁教版54制》

10. 在下列 $ 2×2 $ 的方格中找出规律,则 x 应是(B)。


A.10
B.-2
C.2
D.0

答案： B

11. 观察图中的每一个大三角形中白色三角形的排列规律,则第 5 个大三角形中白色三角形有121个。

答案： 121

12. 国庆期间,小区物业用花盆装点院落。下列的每一个图案都是由若干个花盆组成的正方形图案。

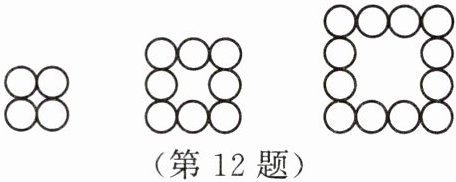
(1)若用 n 表示每条边上(包括两个端点)的花盆数,用 S 表示组成每个图案的花盆数。按上图所表现出来的规律推算,当 $ n = 8 $ 时,S 的值应是多少？
(2)用含 n 的代数式表示 S。

答案：
(1)$S=28$
(2)$S=4n-4$

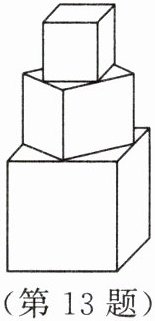
13. 如图所示的是由若干个正方体形状的木块堆成的几何体,平放在桌面上。其中,上面正方体的每个面的面积恰好是下面正方体每个面面积的 $ \dfrac{1}{2} $,最下面的正方体的棱长为 1。
(1)当只有两个正方体放在一起时,这两个正方体露在外面的面积是多少？
(2)当这些正方体露在外面的面积超过 8 时,正方体的个数至少是多少？
(3)按此规律下去,这些正方体露在外面的面积会不会一直增大？如果会,请说明理由；如果不会,请求出不会超过哪个数值。

答案：
(1)7
(2)4个
(3)不会,不会超过9