《2025年同步练习册北京师范大学出版社六年级数学上册鲁教版54制》

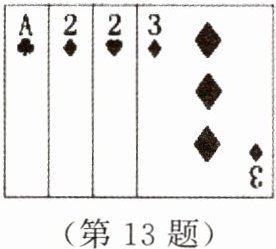
13. 小韦与同学一起玩“24 点”扑克牌游戏,即从一副扑克牌(去掉大、小王)中任意抽出 4 张,根据牌面上的数进行有理数混合运算(每张牌只能用一次),使运算结果等于 24 或 $-24$。小韦抽得的四张牌如图,“我得到 24 点了！”,他的算法是$(1+2)×2^{3}=24$。(A 相当于 1)

答案： $(1+2)×2^{3}=24$

14. 计算：
(1) $(-2)^3 × (-3)^2$；
(2) $(2 - 3)^{225}$；
(3) $(-3)^2 ÷ (-2^4)$；
(4) $-\frac{3^3}{4} + (-1)^{165}$。

答案： 解:
(1)原式$=(-8)×9=-72$。
(2)原式$=(-1)^{225}=-1$。
(3)原式$=9÷(-16)=-\frac{9}{16}$。
(4)原式$=-\frac{27}{4}-1=-7\frac{3}{4}$。

15. 已知 $2^1 = 2$,$2^2 = 4$,$2^3 = 8$,$2^4 = 16$,$2^5 = 32$,…。观察上面式子的规律,试猜想 $2^{1025}$ 的末位数字,并说明理由。

答案： 解:$2^{1025}$的末位数字是2,理由是1025÷4=256……1,又2,4,8,6四个一组循环,$2^{1025}$的末位数字恰好是第1个,即2。

16. 我们平常用的数是十进制的数,如 $2639 = 2 × 10^3 + 6 × 10^2 + 3 × 10^1 + 9$。表示十进制的数要用十个数码：0,1,2,3,4,5,6,7,8,9。在计算机中用的是二进制,只要两个数码：0 和 1。如二进制中 $101 = 1 × 2^2 + 0 × 2^1 + 1$ 等于十进制中的 5,那么二进制中的 1101 等于十进制中的哪个数？

答案： 13

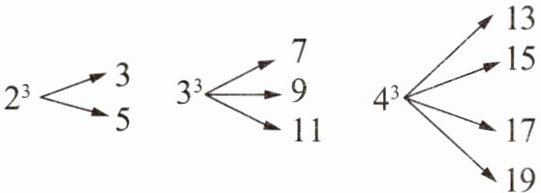
(综合与实践)一个大于 1 的自然数的立方,可以分裂成若干个连续奇数的和,如 $2^3 = 3 + 5$,$3^3 = 7 + 9 + 11$,$4^3 = 13 + 15 + 17 + 19$,…。若 $6^3$ 也按照此规律进行“分裂”,则 $6^3$ 分裂出的奇数中,最大的数是41。

答案： 41