《2025年同步练习册北京师范大学出版社六年级数学上册鲁教版54制》

9. 若 $a,b$ 互为相反数,$c,d$ 互为倒数,则 $\frac{cd}{5}×(a+b)=$0。

答案： 0

10. 写出下面计算过程中每一步的运算依据。
$(-4)×(+8)×(-2.5)×(-125)$
$=-4×8×2.5×125$ (奇数个负因数的积为负数)
$=-4×2.5×8×125$ (乘法交换律)
$=-(4×2.5)×(8×125)$(乘法结合律)
$=-10×1 000= -10 000$。

答案： 奇数个负因数的积为负数   乘法交换律   乘法结合律

11. 计算：
(1) $(-25)×(-2)×(-5)×(-125)×8×4$；
(2) $(0.5-2-\frac{4}{9}+\frac{5}{6}-\frac{7}{12})×(-36)$；
(3) $(+3\frac{1}{7})×(3\frac{1}{7}-7\frac{1}{3})×\frac{7}{22}×\frac{21}{22}$；
(4) $71\frac{15}{16}×(-8)$；
(5) $(-370)×(-\frac{1}{4})+0.25×24.5+(+5\frac{1}{2})×\frac{1}{4}$。

答案：
(1)1 000 000
(2)61
(3)-4
(4)-575$\frac{1}{2}$
(5)100

12. (跨学科)由地理知识可知,各地气温的差异受海拔的影响,海拔每升高 1 m,气温就下降 $0.006^{\circ}C$。现已知重庆的海拔为 260 m,峨眉山的海拔为 3 099 m,则当重庆气温为 $28^{\circ}C$ 时,峨眉山山顶的气温是多少？

答案： 解:从重庆的海拔上升到峨眉山的海拔,气温的变化为(3 099-260)×(-0.006)=-17.034(℃)。所以峨眉山山顶的气温为28-17.034=10.966(℃)。
答:峨眉山山顶的气温是10.996 ℃。

13. 观察下列算式,寻找规律,利用规律解答后面的问题：
$1×3+1= 4= 2^{2}$,$2×4+1= 9= 3^{2}$,$3×5+1= 16= 4^{2}$,$4×6+1= 25= 5^{2}$,…。
(1) 计算：$7×9+1= 64= ($8$)^{2}$。
(2) 请你用找到的规律计算：$(1+\frac{1}{1×3})×(1+\frac{1}{2×4})×(1+\frac{1}{3×5})×…×(1+\frac{1}{9×11})$。
(2)原式=$\frac{1×3+1}{1×3}$×$\frac{2×4+1}{2×4}$×$\frac{3×5+1}{3×5}$×…×$\frac{9×11+1}{9×11}$=$\frac{2^{2}}{1×3}$×$\frac{3^{2}}{2×4}$×$\frac{4^{2}}{3×5}$×…×$\frac{10^{2}}{9×11}$=2×$\frac{10}{11}$=$\frac{20}{11}$。

答案：
(1)8
(2)原式=$\frac{1×3+1}{1×3}$×$\frac{2×4+1}{2×4}$×$\frac{3×5+1}{3×5}$×…×$\frac{9×11+1}{9×11}$=$\frac{2^{2}}{1×3}$×$\frac{3^{2}}{2×4}$×$\frac{4^{2}}{3×5}$×…×$\frac{10^{2}}{9×11}$=2×$\frac{10}{11}$=$\frac{20}{11}$。

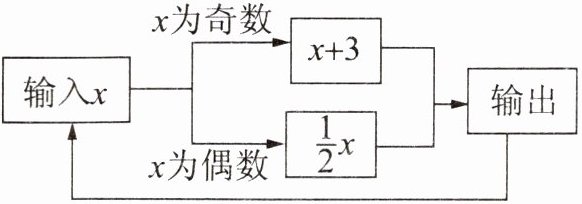
(综合与实践)有一数值转换器,原理如图所示。若开始输入 $x$ 的值是 5,可发现第 1 次输出的结果是 8,第 2 次输出的结果是 4……则第 226 次输出的结果是1。

答案： 1