《2025年同步练习册北京师范大学出版社六年级数学上册鲁教版54制》

1. 计算器上$\boxed{DEL}$键的功能是(D)。
A.开启计算器
B.关闭计算器
C.计算乘方
D.清除当前显示的数或符号

答案： D

2. 计算器上$\boxed{ON/C}$键的功能是(A)。
A.开机与清零
B.交换功能
C.清除当前显示的数或符号
D.关闭计算器

答案： A

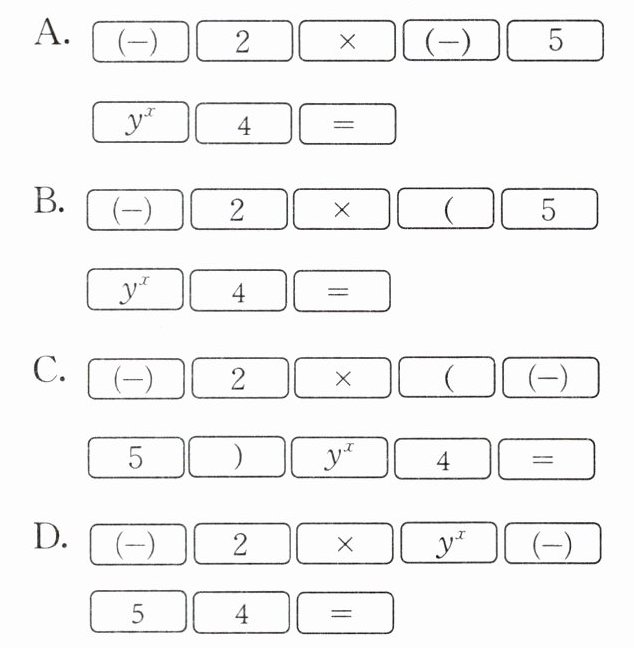
3. 用计算器计算$-2×(-5)^{4}$时,按键的顺序为(C)。

答案： C

4. 使用某种计算器进行计算,按键顺序如下,则计算的结果为(B)。
$\boxed{5}\ \boxed{x^{2}}\ \boxed{+}\ \boxed{2}\ \boxed{y^{x}}\ \boxed{3}\ \boxed{=}$
A.16
B.33
C.37
D.36

答案： B

5. 用操作计算器的方法计算$(3.1×105)×(7.6×108)$,按的第5个键是(C)。
A.$\boxed{0}$
B.$\boxed{5}$
C.$\boxed{×}$
D.$\boxed{1}$

答案： C

6. 用计算器计算：
(1)$2^{3}×(-2.7+0.8)-\frac{3}{4}$；
(2)$-8^{3}-6.4÷(-3.2)$；
(3)$(-2)^{3}÷(-2.5+2.4)-(-1)^{20}$；
(4)$-3^{6}-6.4×(-\frac{1}{8})$。

答案：
(1)-15.95
(2)-510
(3)79
(4)-728.2

7. 用计算器计算下列各式,将结果写在横线上：
(1)$9×9+19=$100,$99×99+199=$10000,$999×999+1999=$1000000,$9999×9999+19999=$100000000；
(2)仔细观察上述各式,根据你所发现的规律直接写出下面算式的运算结果：
$999999×999999+1999999=$1000000000000。

答案： （1）100 10 000 1 000 000 100 000 000（2）1 000 000 000 000

8. 用计算器计算下列各式：
$6×7= $42；
$66×67= $4422；
$666×667= $444222；
$6666×6667= $44442222；
$66666×66667= $4444422222。
观察上述结果,你发现了什么规律？尝试说明理由。
规律：当第一个因数由n个6组成，第二个因数由(n-1)个6和一个7组成时，它们的积由n个4和n个2组成，且4在前，2在后。理由：设第一个因数为$ \underbrace{66\cdots6}_{n个6} $，可表示为$ \frac{2}{3}×(10^n - 1) $，第二个因数为$ \underbrace{66\cdots6}_{(n-1)个6}7 $，可表示为$ \frac{2}{3}×(10^n - 1) + 1 $，两数相乘可得$ \frac{4}{9}×(10^{2n} - 10^n) + \frac{2}{3}×(10^n - 1) = \underbrace{44\cdots4}_{n个4}\underbrace{22\cdots2}_{n个2} $。

答案： 42；4 422；444 222；44 442 222；4 444 422 222 规律略。