《2025年全优新同步八年级数学上册浙教版》

7. 已知点A(a-2,2a+7),点B的坐标为(1,5),直线AB//y轴,则a的值是( )

A.1
B.3
C.-1
D.5

答案： B

8. 已知点P(2a-12,1-a)位于第三象限。
(1)若点P的纵坐标为-3,试求出a的值。
(2)求a的取值范围。
(3)若点P的横、纵坐标都是整数,试求出a的值以及点P的坐标。

答案：
(1)由题意得$1-a=-3$,解得$a=4$。
(2)
∵点$P(2a-12,1-a)$位于第三象限，
$\therefore \left\{\begin{array}{l} 2a-12＜0,\\ 1-a＜0,\end{array}\right. $解得$\left\{\begin{array}{l} a＜6,\\ a＞1.\end{array}\right. \therefore 1＜a＜6$。
(3)
∵点P的横、纵坐标都是整数,
∴a的值为2,3,4,5。
∴点P的坐标为(-8,-1),(-6,-2),(-4,-3)或(-2,-4)。

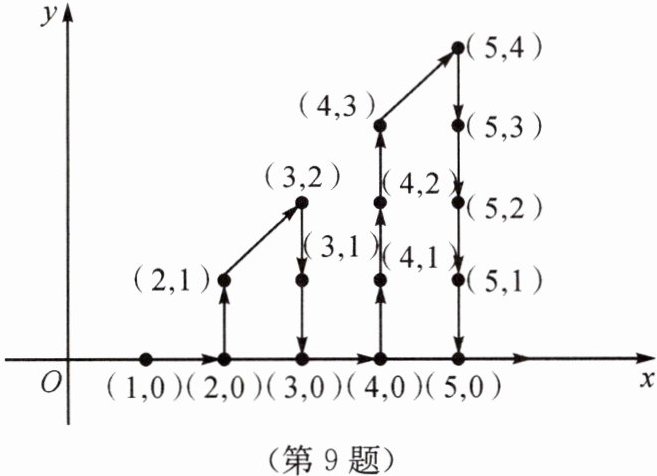
9. 如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,如果(1,0)是第一个点,探究规律如下：
(1)坐标为(3,0)的是第______个点,坐标为(5,0)的是第______个点。
(2)坐标为(7,0)的是第______个点。
(3)第74个点的坐标为______。
]

答案：
(1)6 15
(2)28
(3)(12,7)
【解析】
(1)坐标为(3,0)的点是第$1+2+3=6$个点,坐标是(5,0)的点是第$1+2+3+4+5=15$个点，
(2)坐标为(7,0)的点是第$1+2+3+4+5+6+7=28$个点。
(3)
∵(11,0)是第$1+2+3+\cdots +11=66$个点,(12,11)是第$1+2+3+\cdots +12=78$个点,
∴第74个点是(12,7)。

10. 已知A(4,0),点B在x轴上,且AB= 5。
(1)直接写出点B的坐标。
(2)若点C在y轴上,且S△ABC= 10,求点C的坐标。

答案：
(1)
∵A(4,0),点B在x轴上,AB= 5，
∴B(-1,0)或(9,0)。
(2)
∵AB= 5,C是y轴上一点,$S_{\triangle ABC}= 10$，
$\therefore S_{\triangle ABC}=\frac {1}{2}×AB×OC$。
$\therefore 10=\frac {1}{2}×5×OC$。$\therefore OC=4$。
∴点C坐标为(0,4)或(0,-4)。

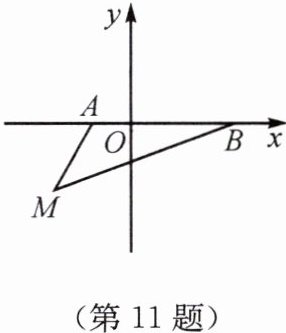
11. 如图所示,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b-3)^2= 0。
(1)填空：a= ______,b= ______。
(2)如果在第三象限内有一点M(-2,m),请用含m的代数式表示△ABM的面积。
(3)在(2)的条件下,当m= $-\frac{3}{2}$时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标。
]

答案：

(1)-1 3
(2)过点M作$MN⊥x$轴于点N。
∵A(-1,0),B(3,0),
∴AB=1+3=4。
∵点M(-2,m)在第三象限,
∴MN=|m|=-m。
$\therefore S_{\triangle ABM}=\frac {1}{2}AB\cdot MN=\frac {1}{2}×4×(-m)=-2m$。
(3)当$m= -\frac{3}{2}$时,$M(-2,-\frac{3}{2})$，
$\therefore S_{\triangle ABM}=-2×(-\frac{3}{2})=3$。
点P有两种情况:①如图1所示,当点P在y轴正半轴上时,设点P(0,k)。
$S_{\triangle BMP}=5×(\frac{3}{2}+k)-\frac{1}{2}×2×(\frac{3}{2}+k)-\frac{1}{2}×5×\frac{3}{2}-\frac{1}{2}×3×k=\frac{5}{2}k+\frac{9}{4}$。
∵$S_{\triangle BMP}=S_{\triangle ABM}$,$\therefore \frac{5}{2}k+\frac{9}{4}=3$,解得k=0.3。
∴点P的坐标为(0,0.3)。
②如图2所示,当点P在y轴负半轴上时,设点P(0,n)。
$S_{\triangle BMP}=-5n-\frac{1}{2}×2×(-n-\frac{3}{2})-\frac{1}{2}×5×\frac{3}{2}-\frac{1}{2}×3×(-n)=-\frac{5}{2}n-\frac{9}{4}$。
∵$S_{\triangle BMP}=S_{\triangle ABM}$,$\therefore -\frac{5}{2}n-\frac{9}{4}=3$,解得n=-2.1。
∴点P的坐标为(0,-2.1)。
综上所述,点P的坐标为(0,0.3)或(0,-2.1)。