《2025年全优新同步八年级数学上册浙教版》

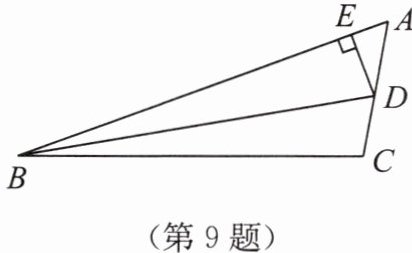
9. 如图所示,BD是∠ABC的平分线,DE⊥AB于点$E,S△ABC= 33 cm^2,AB= 16 cm,BC= 14 cm,$则DE的长是( )


A.2 cm
B.3 cm
C.2.4 cm
D.2.2 cm

答案：
D【解析】如图所示，过点D作DF⊥BC交BC的延长线于点F。
∵BD是∠ABC的平分线，DE⊥AB，
∴DE=DF。
∵S△ABC=33cm²，AB=16cm，BC=14cm，
∴S△ABC=S△ABD+S△BCD=1/2AB·DE+1/2BC·DF=1/2DE·(AB+BC)=1/2DE×(16+14)=33cm²，解得DE=2.2(cm)。故选D。

10. 如图所示,在△ABC中,∠BAC= 90°,∠ABC的平分线交AC于点D,DE⊥BC于点E,若△ABC与△CDE的周长分别为13和3,则AB的长为( )


A.10
B.16
C.8
D.5

答案： D【解析】
∵∠BAC=90°，BD平分∠ABC，DE⊥BC，
∴AD=DE，∠ABD=∠EBD，∠A=∠BED=90°。
∵BD=BD，
∴△ABD≌△EBD。
∴AB=BE。
∵△ABC与△CDE的周长分别为13和3，
∴AB+BC+AC=AB+BE+EC+AC=13，DE+DC+EC=AD+DC+EC=AC+EC=3。
∴AB+BE=10。
∴AB=BE=5。故选D。

11. 如图所示,点P是△ABC的内角∠ABC与它的外角∠ACD的平分线的交点,已知点P到AC的距离为5,则点P到直线AB的距离为______。

答案： 5

12. 如图所示,在△ABC中,AB= AC,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为E,F。
(1)若∠BDE= 55°,求∠BAC的度数。
(2)求证:DE= DF。

答案：
(1)
∵DE⊥AB，
∴∠BED=90°。
∵∠BDE=55°，
∴∠B=35°。
∵AB=AC，
∴∠C=∠B=35°。
∴∠BAC=110°。
(2)连结AD。
∵D是BC的中点，
∴BD=CD。
∵AB=AC，AD=AD，
∴△ABD≌△ACD。
∴∠DAB=∠DAC。
∵DE⊥AB，DF⊥AC，
∴DE=DF。

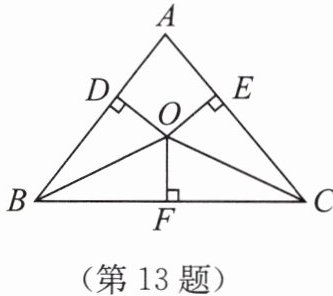
13. 如图所示,在△ABC中,O为∠ABC,∠ACB的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,垂足分别为D,E,F。
(1)判断OD与OE是否相等,并说明理由。
(2)若△ABC的周长是30,且OF= 4,求△ABC的面积。

答案：
(1)OD=OE。理由如下：
∵BO平分∠ABC，OD⊥AB，OF⊥BC，
∴OD=OF。
∵CO平分∠ACB，OE⊥AC，OF⊥BC，
∴OE=OF。
∴OD=OE。
(2)连结OA。
∵△ABC的周长是30，
∴AB+BC+AC=30。
∵OF=4，
∴OD=OE=OF=4。
∴△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积=1/2AB·OD+1/2BC·OF+1/2AC·OE=1/2OD·(AB+BC+AC)=1/2×4×30=60。

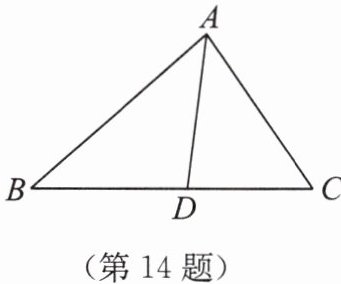
14. 如图所示,在△ABC中,AD平分∠BAC。
(1)求证:S△ABD:S△ADC= AB:AC。
(2)在△ABC中,AB= 5,AC= 4,BC= 6,求DC的长。

答案：

(1)如图所示，过点D作DE⊥AB于点E，DF⊥AC于点F。
∵AD平分∠BAC，
∴DE=DF。
∴S△ABD:S△ADC=1/2AB·DE:1/2AC·DF=AB:AC。

(2)
∵S△ABD:S△ADC=AB:AC，S△ABD:S△ADC=BD:CD，
∴AB:AC=BD:CD，即5:4=BD:CD。
∴BD=5/4CD。
∵BD+CD=BC=6，
∴5/4CD+CD=6。
∴CD=8/3。