《2025年全优新同步八年级数学上册浙教版》

9. 【宜昌】如图所示,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从$P_1,P_2,P_3,P_4$四个点中找出符合条件的点P,则点P有 ( )

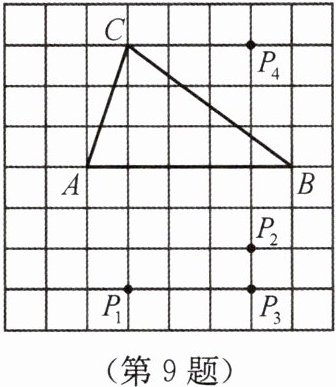
A.1个
B.2个
C.3个
D.4个

答案： C

10. 已知△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若这两个三角形全等,则x为______。

答案： 3【解析】
∵△ABC三边长分别为3,5,7，△DEF三边长分别为3,3x-2,2x-1，这两个三角形全等，
∴3x-2=7,2x-1=5，解得x=3；或3x-2=5,2x-1=7，这样的x不存在。
∴x=3。

11. 如图所示,已知AD= BC,AE= CF,DF= BE,找出图中一对全等的三角形,并说明理由。

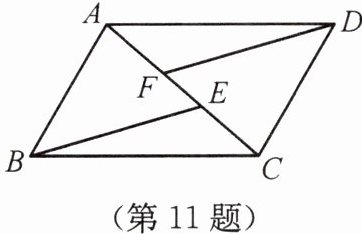
答案： △ADF和△CBE全等。理由如下：
∵AE=CF，
∴AE-EF=CF-EF，即AF=CE。在△ADF和△CBE中，
∵{AD=BC,AF=CE,DF=BE,
∴△ADF≌△CBE(SSS)。

12. 工人师傅常用角尺平分一个任意角。做法如下：如图所示,∠AOB是一个任意角,在边OA,OB上分别取OM= ON,移动角尺,使角尺两边相等的刻度分别与点M,N重合,过角尺顶点C作射线OC即可得∠AOC= ∠BOC。请说明理由。

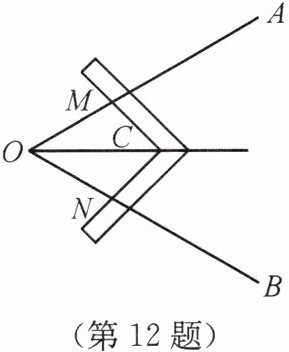
答案： 在△MOC和△NOC中，
∵{OM=ON,CM=CN,OC=OC,
∴△MOC≌△NOC(SSS)。
∴∠AOC=∠BOC。

13. 如图所示,D是BC上一点,AB= AD,BC= DE,AC= AE,AC与DE交于点F,求证：∠CDE= ∠BAD。

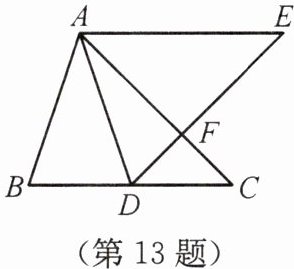
答案： 在△ABC和△ADE中，
∵{AB=AD,BC=DE,AC=AE,
∴△ABC≌△ADE(SSS)。
∴∠BAC=∠DAE，∠C=∠E。
∴∠BAC-∠DAC=∠DAE-∠DAC。
∴∠BAD=∠CAE。
∵∠CAE+∠E+∠AFE=∠CDE+∠C+∠CFD，又
∵∠AFE=∠CFD，∠C=∠E，
∴∠CAE=∠CDE=∠BAD。