《2025年全优新同步八年级数学上册浙教版》

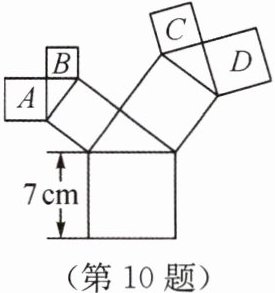
10.如图所示,图中所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为 ( )
$A.3cm^2 B.4cm^2 C.7cm^2 D.49cm^2$
]

答案： D

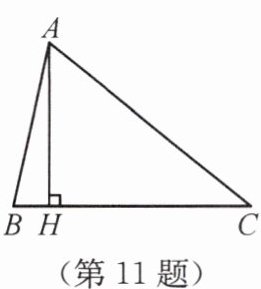
11.如图所示,在△ABC中,∠ABC= 2∠ACB,AH⊥BC于点H,若AB= 5,BH= 1,则BC= ______。
]

答案： 7

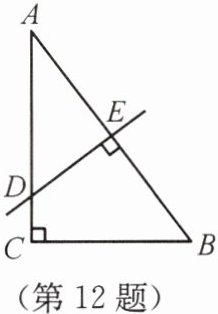
12.如图所示,在Rt△ABC中,∠C= 90°,AC= 10,BC= 8,AB的垂直平分线分别交AC,AB于点D,E,则AD的长度为______。
]

答案： 8.2【解析】连结BD。
∵DE是线段AB的垂直平分线，
∴$AD=BD$。
设$AD=BD=x$，则$CD=AC - AD=10 - x$。
在$Rt△BCD$中，由勾股定理得$8^{2}+(10 - x)^{2}=x^{2}$，
解得$x=8.2$。

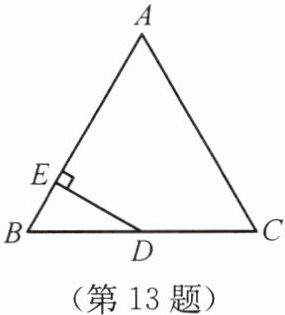
13.如图所示,在△ABC中,AB= AC= 13,BC= 10,D为BC的中点,DE⊥AB,垂足为E,求DE的长。
]

答案：
如图所示，连结AD。
∵在$△ABC$中，$AB=AC=13,BC=10$，D为BC中点，
∴$AD⊥BC,BD=\frac {1}{2}BC=5$。

∴$AD=\sqrt {AB^{2}-BD^{2}}=12$。
∵$DE⊥AB$，
∴$\frac {1}{2}BD\cdot AD=\frac {1}{2}AB\cdot ED$。
∴$ED=\frac {BD\cdot AD}{AB}=\frac {5×12}{13}=\frac {60}{13}$。

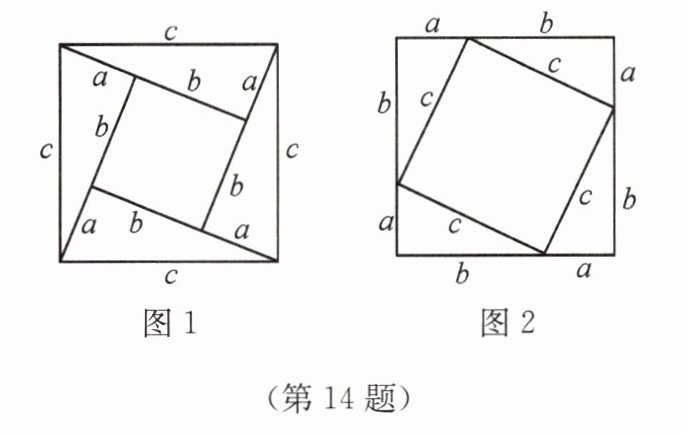
14.如图所示,图1和图2都是用四个全等的直角三角形围成的图形,请你选择图1或图2中的有关面积的等量关系证明数学中的勾股定理。
]

答案： ①选择图1。
如图1所示，大正方形的面积为$c^{2}$，用三角形的面积与边长为$(a - b)$的正方形的面积表示为$4×\frac {1}{2}ab+(a - b)^{2}$，
∴$c^{2}=4×\frac {1}{2}ab+(a - b)^{2}$，化简得$a^{2}+b^{2}=c^{2}$。
②选择图2。
如图2所示，大正方形的面积为$(a + b)^{2}$，用三角形的面积与边长为c的正方形的面积表示为$4×\frac {1}{2}ab+c^{2}$，
∴$(a + b)^{2}=4×\frac {1}{2}ab+c^{2}$，化简得$a^{2}+b^{2}=c^{2}$。

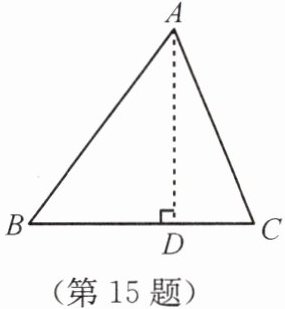
15.在△ABC中,AB= 15,BC= 14,AC= 13,求△ABC的面积。
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程。
①作AD⊥BC于点D,设BD= x,用含x的代数式表示CD。
②根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x的值。
③利用勾股定理求出AD的长,再计算出三角形的面积。
]

答案： 在$△ABC$中，$AB=15,BC=14,AC=13$，
设$BD=x$，则$CD=14 - x$。
由勾股定理得$AD^{2}=AB^{2}-BD^{2}=15^{2}-x^{2},AD^{2}=AC^{2}-CD^{2}=13^{2}-(14 - x)^{2}$，
∴$15^{2}-x^{2}=13^{2}-(14 - x)^{2}$，解得$x=9$。
∴$AD=12$。
∴$S_{△ABC}=\frac {1}{2}BC\cdot AD=\frac {1}{2}×14×12=84$。