《2025年全优新同步八年级数学上册浙教版》

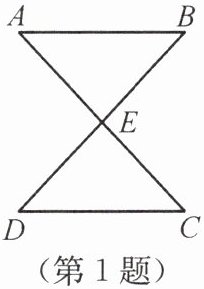
1. 如图所示,若AB//CD,且AB= CD,则△ABE≌△CDE的根据 ( )

A.只能用ASA
B.只能用SAS
C.只能用AAS
D.能用ASA或AAS

答案： B

2. 如图所示,要测量河两岸相对的两点A,B的距离,先过点B作BF⊥AB,在BF上找点D,过点D作DE⊥BF,再取BD的中点C,连结AC并延长,与DE交于点E,此时测得DE的长度就是AB的长度。这里判定△ABC和△EDC全等的依据是( )

A.ASA
B.SAS
C.SSS
D.AAS

答案： A

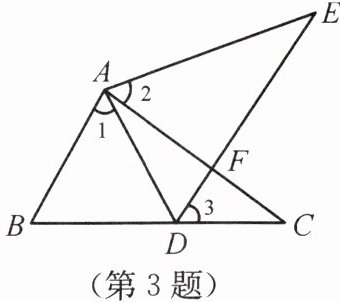
3. 如图所示,点E在△ABC外部,点D在BC边上,DE交AC于点F,如果∠1= ∠2,∠E= ∠C,AE= AC,那么 ( )

A.△ABC≌△AFE
B.△AFE≌△ADC
C.△AFE≌△DFC
D.△ABC≌△ADE

答案： D

4. 如图所示,已知∠A= ∠D,EF//BC,若再添加一个适当的条件,使得△ABC≌△DEF,则添加的这个条件可以是______。(只要填上一个满足的条件即可)

答案： AC=DF(或 AF=CD)

5. 如图所示,∠AOB= 90°,OA= OB,直线l经过点O,分别过A,B两点作AC⊥l于点C,BD⊥l于点D。若AC= 10,BD= 6,则CD= ______。

答案： 4

6. 如图所示,已知点A,D,C在同一直线上,AB//EC,AC= CE,∠B= ∠EDC。求证：BC= DE。

答案：
∵AB//EC,
∴∠A=∠DCE。
在△ABC 和△CDE 中,
∵{∠B=∠EDC,∠A=∠DCE,AC=CE,
∴△ABC≌△CDE(AAS)。
∴BC=DE。

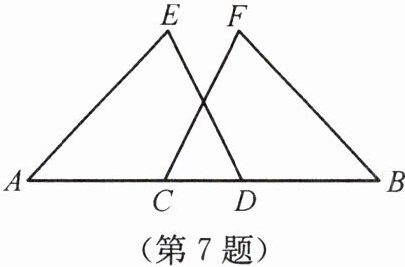
7.【衡阳】如图所示,A,C,D,B四点共线,且AC= BD,∠A= ∠B,∠ADE= ∠BCF,求证：DE= CF。

答案：
∵AC=BD,
∴AC+CD=BD+CD。
∴AD=BC。
在△AED 和△BFC 中,
∵{∠A=∠B,AD=BC,∠ADE=∠BCF,
∴△AED≌△BFC(ASA)。
∴DE=CF。