11.已知命题"等腰三角形两腰上的高线相等",它的逆命题是 ,该逆命题是 命题。(填"真"或"假")
答案:
如果一个三角形两条边上的高线相等,那么这个三角形是等腰三角形 真
12.写出下列命题的逆命题,并判断逆命题的真假。
(1)若x= 2,则|x|= 2。
(2)对顶角相等。
(3)等边三角形的三个内角都是60°。
(1)若x= 2,则|x|= 2。
(2)对顶角相等。
(3)等边三角形的三个内角都是60°。
答案:
(1)逆命题:若$|x|=2$,则$x=2$,是假命题。
(2)逆命题:相等的两个角是对顶角,是假命题。
(3)逆命题:三个角都是$60^{\circ}$的三角形是等边三角形,是真命题。
(1)逆命题:若$|x|=2$,则$x=2$,是假命题。
(2)逆命题:相等的两个角是对顶角,是假命题。
(3)逆命题:三个角都是$60^{\circ}$的三角形是等边三角形,是真命题。
13.写出下列命题的逆命题,并判断逆命题的真假。若逆命题是真命题,请加以证明;若逆命题是假命题,请举出反例。
(1)如果a,b都是无理数,那么ab也是无理数。
(2)等腰三角形两腰上的高线相等。
(1)如果a,b都是无理数,那么ab也是无理数。
(2)等腰三角形两腰上的高线相等。
答案:
(1)逆命题:如果$ab$是无理数,那么$a,b$都是无理数。此逆命题为假命题。反例:当$a=1,b=\sqrt{2}$时,$ab=\sqrt{2}$是无理数,而$a$不是无理数。
(2)逆命题:如果一个三角形两边上的高线相等,则这个三角形是等腰三角形。此逆命题是真命题。证明如下:
如图所示,已知在$\triangle ABC$中,$BE\perp AC$于点$E$,
$CF\perp AB$于点$F$,且$BE=CF$。
求证:$AB=AC$。
证明:$\because S_{\triangle ABC}=\frac{1}{2}AB\cdot CF=\frac{1}{2}AC\cdot BE$,又$\because BE=CF$,$\therefore AB=AC$。$\therefore \triangle ABC$是等腰三角形。

(1)逆命题:如果$ab$是无理数,那么$a,b$都是无理数。此逆命题为假命题。反例:当$a=1,b=\sqrt{2}$时,$ab=\sqrt{2}$是无理数,而$a$不是无理数。
(2)逆命题:如果一个三角形两边上的高线相等,则这个三角形是等腰三角形。此逆命题是真命题。证明如下:
如图所示,已知在$\triangle ABC$中,$BE\perp AC$于点$E$,
$CF\perp AB$于点$F$,且$BE=CF$。
求证:$AB=AC$。
证明:$\because S_{\triangle ABC}=\frac{1}{2}AB\cdot CF=\frac{1}{2}AC\cdot BE$,又$\because BE=CF$,$\therefore AB=AC$。$\therefore \triangle ABC$是等腰三角形。

14.写出命题"如果一个三角形是直角三角形,那么它的两个锐角的平分线所夹的锐角是45°"的逆命题,并证明这个命题是真命题。
答案:
逆命题:如果一个三角形的两个角的平分线所夹的锐角是$45^{\circ}$,那么这个三角形是直角三角形。
证明:如图所示,已知在$\triangle ABC$中,$BE$是$\angle ABC$的平分线,交$AC$于点$E$,$AD$是$\angle CAB$的平分线,交$BC$于点$D$,$BE$和$AD$相交于点$O$,且$\angle EOA=45^{\circ}$。求证:$\triangle ABC$是直角三角形。
证明:$\because BE$是$\angle ABC$的平分线,$AD$是$\angle CAB$的平分线,$\therefore \angle OAB=\frac{1}{2}\angle CAB$,$\angle OBA=\frac{1}{2}\angle CBA$。$\therefore \angle OAB+\angle OBA=\frac{1}{2}(\angle CAB+\angle CBA)$。$\therefore 180^{\circ}-\angle AOB=\frac{1}{2}(180^{\circ}-\angle C)$。$\therefore \angle AOB=90^{\circ}+\frac{1}{2}\angle C$。$\because \angle EOA=45^{\circ}$,$\therefore \angle AOB=135^{\circ}=90^{\circ}+\frac{1}{2}\angle C$。$\therefore \angle C=90^{\circ}$。$\therefore \triangle ABC$是直角三角形。

逆命题:如果一个三角形的两个角的平分线所夹的锐角是$45^{\circ}$,那么这个三角形是直角三角形。
证明:如图所示,已知在$\triangle ABC$中,$BE$是$\angle ABC$的平分线,交$AC$于点$E$,$AD$是$\angle CAB$的平分线,交$BC$于点$D$,$BE$和$AD$相交于点$O$,且$\angle EOA=45^{\circ}$。求证:$\triangle ABC$是直角三角形。
证明:$\because BE$是$\angle ABC$的平分线,$AD$是$\angle CAB$的平分线,$\therefore \angle OAB=\frac{1}{2}\angle CAB$,$\angle OBA=\frac{1}{2}\angle CBA$。$\therefore \angle OAB+\angle OBA=\frac{1}{2}(\angle CAB+\angle CBA)$。$\therefore 180^{\circ}-\angle AOB=\frac{1}{2}(180^{\circ}-\angle C)$。$\therefore \angle AOB=90^{\circ}+\frac{1}{2}\angle C$。$\because \angle EOA=45^{\circ}$,$\therefore \angle AOB=135^{\circ}=90^{\circ}+\frac{1}{2}\angle C$。$\therefore \angle C=90^{\circ}$。$\therefore \triangle ABC$是直角三角形。

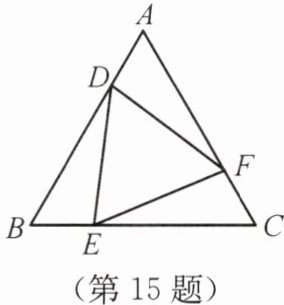
15.如图所示,△ABC是等边三角形。
(1)如果AD= BE= CF,求证:△DEF是等边三角形。
(2)请问(1)的逆命题成立吗?若成立,请加以证明;若不成立,请用反例说明。
(1)如果AD= BE= CF,求证:△DEF是等边三角形。
(2)请问(1)的逆命题成立吗?若成立,请加以证明;若不成立,请用反例说明。

答案:
(1)$\because \triangle ABC$是等边三角形,$\therefore \angle A=\angle B=\angle C=60^{\circ}$,$AC=AB=BC$。$\because AD=BE=CF$,$\therefore AC - CF=BC - BE=AB - AD$。$\therefore AF=EC=BD$。在$\triangle ADF$和$\triangle BED$中,$\because \left\{\begin{array}{l}AD=BE,\\ \angle A=\angle B,\\ AF=BD,\end{array}\right.$$\therefore \triangle ADF\cong \triangle BED(SAS)$。$\therefore DF=DE$。同理可得$DE=EF$。$\therefore \triangle DEF$是等边三角形。
(2)
(1)的逆命题成立。
已知:$\triangle ABC$,$\triangle DEF$都是等边三角形。求证:$AD=BE=CF$。
证明:$\because \triangle DEF$是等边三角形,$\therefore \angle EDF=\angle EFD=\angle DEF=60^{\circ}$,$DF=EF=DE$。$\because \triangle ABC$是等边三角形,$\therefore \angle A=\angle B=\angle C=60^{\circ}$。$\therefore \angle ADF+\angle AFD=120^{\circ}$,$\angle ADF+\angle BDE=120^{\circ}$,$\angle BDE+\angle DEB=120^{\circ}$,$\angle DEB+\angle FEC=120^{\circ}$。$\therefore \angle AFD=\angle BDE=\angle FEC$。在$\triangle ADF$和$\triangle BED$中,$\because \left\{\begin{array}{l}\angle A=\angle B,\\ \angle AFD=\angle BDE,\\ DF=ED,\end{array}\right.$$\therefore \triangle ADF\cong \triangle BED(AAS)$。$\therefore AD=BE$。同理可得$BE=CF$。$\therefore AD=BE=CF$。
(1)$\because \triangle ABC$是等边三角形,$\therefore \angle A=\angle B=\angle C=60^{\circ}$,$AC=AB=BC$。$\because AD=BE=CF$,$\therefore AC - CF=BC - BE=AB - AD$。$\therefore AF=EC=BD$。在$\triangle ADF$和$\triangle BED$中,$\because \left\{\begin{array}{l}AD=BE,\\ \angle A=\angle B,\\ AF=BD,\end{array}\right.$$\therefore \triangle ADF\cong \triangle BED(SAS)$。$\therefore DF=DE$。同理可得$DE=EF$。$\therefore \triangle DEF$是等边三角形。
(2)
(1)的逆命题成立。
已知:$\triangle ABC$,$\triangle DEF$都是等边三角形。求证:$AD=BE=CF$。
证明:$\because \triangle DEF$是等边三角形,$\therefore \angle EDF=\angle EFD=\angle DEF=60^{\circ}$,$DF=EF=DE$。$\because \triangle ABC$是等边三角形,$\therefore \angle A=\angle B=\angle C=60^{\circ}$。$\therefore \angle ADF+\angle AFD=120^{\circ}$,$\angle ADF+\angle BDE=120^{\circ}$,$\angle BDE+\angle DEB=120^{\circ}$,$\angle DEB+\angle FEC=120^{\circ}$。$\therefore \angle AFD=\angle BDE=\angle FEC$。在$\triangle ADF$和$\triangle BED$中,$\because \left\{\begin{array}{l}\angle A=\angle B,\\ \angle AFD=\angle BDE,\\ DF=ED,\end{array}\right.$$\therefore \triangle ADF\cong \triangle BED(AAS)$。$\therefore AD=BE$。同理可得$BE=CF$。$\therefore AD=BE=CF$。
查看更多完整答案,请扫码查看


