1. 下列各式中,属于一元一次不等式的是( )
A.5+4>8
B.2x-1
C.2x≤5
D.$\frac{1}{x}-3x \geq 0$
A.5+4>8
B.2x-1
C.2x≤5
D.$\frac{1}{x}-3x \geq 0$
答案:
C
2. 根据“x与6的差大于3”列出的不等式正确的是( )
A.x-6≥3
B.x-6≤3
C.x-6>3
D.x-6<3
A.x-6≥3
B.x-6≤3
C.x-6>3
D.x-6<3
答案:
C
3. 解不等式$-\frac{2x}{3} > \frac{3}{2}$,正确的结果是( )
A.$x < -\frac{9}{4}$
B.$x > -\frac{9}{4}$
C.x > -1
D.x < -1
A.$x < -\frac{9}{4}$
B.$x > -\frac{9}{4}$
C.x > -1
D.x < -1
答案:
A
4.【江西】将不等式3x-2<1的解表示在数轴上,正确的是( )
]
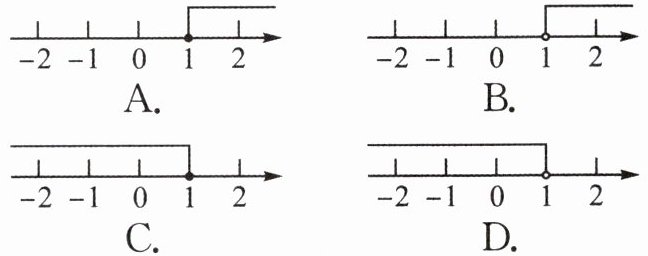
]
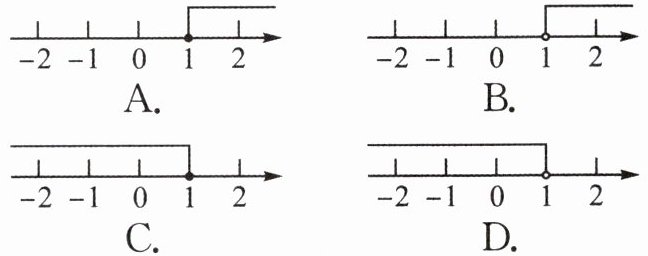
答案:
D [解析]移项,得3x<3。两边都除以3,得x<1。故选D。
5.【安徽】不等式x-2≥1的解是______。
答案:
x≥3
6. 根据数量关系列不等式:x的2倍与3的差大于7:______。
答案:
2x−3>7
7. 不等式-4x≥-12的正整数解为______。
答案:
1,2,3
8. 当x______时,代数式-3x+5的值不大于2。
答案:
≥1
9. 用适当的不等式表示下列数量关系:
(1)x减去3大于10。
(2)x的3倍与5的差是负数。
(3)x的2倍与1的和是非负数。
(4)y的3倍与9的差不大于-1。
(1)x减去3大于10。
(2)x的3倍与5的差是负数。
(3)x的2倍与1的和是非负数。
(4)y的3倍与9的差不大于-1。
答案:
(1)x−3>10。
(2)3x−5<0。
(3)2x+1≥0。
(4)3y−9≤−1。
(1)x−3>10。
(2)3x−5<0。
(3)2x+1≥0。
(4)3y−9≤−1。
10. 解下列不等式,并将解在数轴上表示出来。
(1)3a+3≥1。
(2)-3x-7<0。
(3)5x-1≤3x+3。
(4)-2+x>3x+2。
(1)3a+3≥1。
(2)-3x-7<0。
(3)5x-1≤3x+3。
(4)-2+x>3x+2。
答案:
(1)移项,得3a≥1−3。合并同类项,得3a≥−2。两边同乘$\frac{1}{3}$,得a≥$-\frac{2}{3}$。将解表示在数轴上如下:
(2)移项,得−3x<7。两边同乘$-\frac{1}{3}$,得x>$-\frac{7}{3}$。将解表示在数轴上如下:
(3)移项,得5x−3x≤3+1。合并同类项,得2x≤4。两边同除以2,得x≤2。将解表示在数轴上如下:
(4)移项,得x−3x>2+2。合并同类项,得−2x>4。两边同除以−2,得x<−2。将解表示在数轴上如下:
(1)移项,得3a≥1−3。合并同类项,得3a≥−2。两边同乘$\frac{1}{3}$,得a≥$-\frac{2}{3}$。将解表示在数轴上如下:

(2)移项,得−3x<7。两边同乘$-\frac{1}{3}$,得x>$-\frac{7}{3}$。将解表示在数轴上如下:

(3)移项,得5x−3x≤3+1。合并同类项,得2x≤4。两边同除以2,得x≤2。将解表示在数轴上如下:

(4)移项,得x−3x>2+2。合并同类项,得−2x>4。两边同除以−2,得x<−2。将解表示在数轴上如下:

查看更多完整答案,请扫码查看


