13. 对于平面直角坐标系中的任意两点$A(x_1,y_1),B(x_2,y_2),$定义一种新运算“*”为:$(x_1,y_1)*(x_2,y_2)= (x_1y_2,x_2y_1)。$如果$A(x_1,y_1)$在第二象限$,B(x_2,y_2)$在第三象限,那么A*B在第______象限。
答案:
四
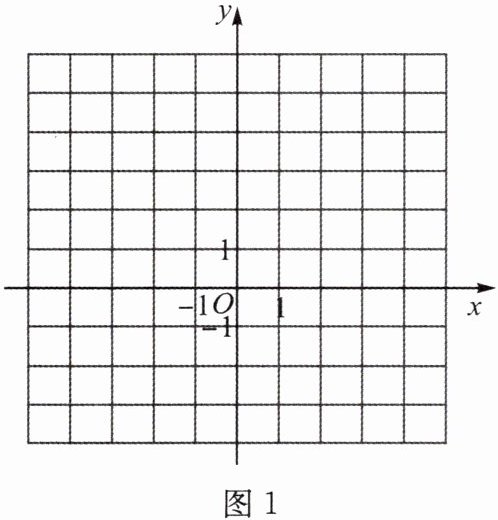
14. (1)在图1的平面直角坐标系中标出下列点:(-3,-2),(-2,-1),(-1,0),(0,1),(1,2),(2,3)。
(2)观察你在图1中所标的点的规律,若点(100,y)也符合(1)中所标的点的排列规律,y的值是多少?
(3)若点(a,b)也符合你在图1所标的点的排列规律,a和b应满足什么关系?
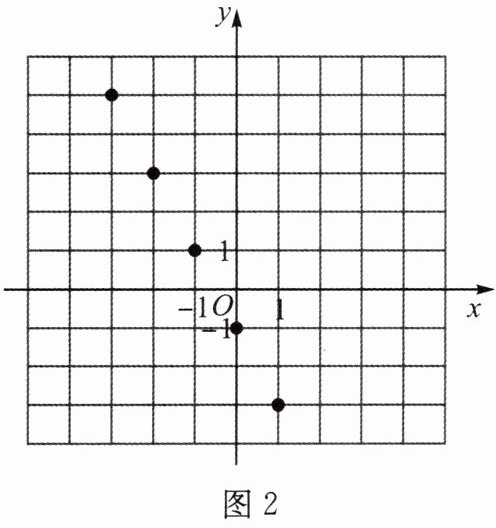
(4)观察图2,若点(m,n)也符合此图的点的排列规律,m和n应满足什么关系?
(2)观察你在图1中所标的点的规律,若点(100,y)也符合(1)中所标的点的排列规律,y的值是多少?
(3)若点(a,b)也符合你在图1所标的点的排列规律,a和b应满足什么关系?
(4)观察图2,若点(m,n)也符合此图的点的排列规律,m和n应满足什么关系?


答案:
(1)如图所示。

(2)根据规律,纵坐标比横坐标大1,
∴$y=100+1=101$。
(3)$a+1=b$。
(4)$2m+n=-1$。
(1)如图所示。

(2)根据规律,纵坐标比横坐标大1,
∴$y=100+1=101$。
(3)$a+1=b$。
(4)$2m+n=-1$。
15. 已知点P(a-2,2a+8),分别根据下列条件,求出点P的坐标。
(1)点P在x轴上。
(2)点P在y轴上。
(3)点Q的坐标为(1,5),直线PQ//y轴。
(4)点P到x轴、y轴的距离相等。
(1)点P在x轴上。
(2)点P在y轴上。
(3)点Q的坐标为(1,5),直线PQ//y轴。
(4)点P到x轴、y轴的距离相等。
答案:
(1)
∵点P(a-2,2a+8)在x轴上,
∴$2a+8=0$,解得$a=-4$。$a-2=-4-2=-6$,则P(-6,0)。
(2)
∵点P(a-2,2a+8)在y轴上,
∴$a-2=0$,解得$a=2$。$2a+8=2×2+8=12$,则P(0,12)。
(3)
∵点Q的坐标为(1,5),直线PQ$// y$轴,
∴$a-2=1$,解得$a=3$。$2a+8=14$,则P(1,14)。
(4)
∵点P到x轴、y轴的距离相等,
∴$a-2=2a+8$或$a-2=-(2a+8)$,解得$a=-10$或$a=-2$。当$a=-10$时,$a-2=-12$,$2a+8=-12$,则P(-12,-12)。当$a=-2$时,$a-2=-4$,$2a+8=4$,则P(-4,4)。综上所述,P(-12,-12)或(-4,4)。
(1)
∵点P(a-2,2a+8)在x轴上,
∴$2a+8=0$,解得$a=-4$。$a-2=-4-2=-6$,则P(-6,0)。
(2)
∵点P(a-2,2a+8)在y轴上,
∴$a-2=0$,解得$a=2$。$2a+8=2×2+8=12$,则P(0,12)。
(3)
∵点Q的坐标为(1,5),直线PQ$// y$轴,
∴$a-2=1$,解得$a=3$。$2a+8=14$,则P(1,14)。
(4)
∵点P到x轴、y轴的距离相等,
∴$a-2=2a+8$或$a-2=-(2a+8)$,解得$a=-10$或$a=-2$。当$a=-10$时,$a-2=-12$,$2a+8=-12$,则P(-12,-12)。当$a=-2$时,$a-2=-4$,$2a+8=4$,则P(-4,4)。综上所述,P(-12,-12)或(-4,4)。
16. 在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称Q是点P的“a级关联点”(其中a为常数,且a≠0)。例如,点P(1,4)的“2级关联点”为Q(2×1+4,1+2×4),即Q(6,9)。
(1)若点P的坐标为(-1,5),则它的“3级关联点”的坐标为______。
(2)若点P的“5级关联点”的坐标为(9,-3),求点P的坐标。
(3)若点P(m-1,2m)的“-3级关联点”P'位于坐标轴上,求点P'的坐标。
(1)若点P的坐标为(-1,5),则它的“3级关联点”的坐标为______。
(2)若点P的“5级关联点”的坐标为(9,-3),求点P的坐标。
(3)若点P(m-1,2m)的“-3级关联点”P'位于坐标轴上,求点P'的坐标。
答案:
(1)$3×(-1)+5=2$,$-1+3×5=14$,
∴若点P的坐标为(-1,5),则它的“3级关联点”的坐标为(2,14)。故答案为:(2,14)。
(2)设点P的坐标为(a,b)。由题意可知$\left\{\begin{array}{l} 5a+b=9\\ a+5b=-3\end{array}\right. $,解得$\left\{\begin{array}{l} a=2\\ b=-1\end{array}\right. $。
∴点P的坐标为(2,-1)。
(3)
∵点P(m-1,2m)的“-3级关联点”为$P'(-3(m-1)+2m,m-1+(-3)×2m)$,①点$P'$位于x轴上,
∴$m-1+(-3)×2m=0$,解得$m=-\frac {1}{5}$。
∴$-3(m-1)+2m=\frac {16}{5}$。
∴$P'(\frac {16}{5},0)$。
②点$P'$位于y轴上,
∴$-3(m-1)+2m=0$,解得$m=3$。
∴$m-1+(-3)×2m=-16$。
∴$P'(0,-16)$。综上所述,点$P'$的坐标为$(\frac {16}{5},0)$或(0,-16)。
(1)$3×(-1)+5=2$,$-1+3×5=14$,
∴若点P的坐标为(-1,5),则它的“3级关联点”的坐标为(2,14)。故答案为:(2,14)。
(2)设点P的坐标为(a,b)。由题意可知$\left\{\begin{array}{l} 5a+b=9\\ a+5b=-3\end{array}\right. $,解得$\left\{\begin{array}{l} a=2\\ b=-1\end{array}\right. $。
∴点P的坐标为(2,-1)。
(3)
∵点P(m-1,2m)的“-3级关联点”为$P'(-3(m-1)+2m,m-1+(-3)×2m)$,①点$P'$位于x轴上,
∴$m-1+(-3)×2m=0$,解得$m=-\frac {1}{5}$。
∴$-3(m-1)+2m=\frac {16}{5}$。
∴$P'(\frac {16}{5},0)$。
②点$P'$位于y轴上,
∴$-3(m-1)+2m=0$,解得$m=3$。
∴$m-1+(-3)×2m=-16$。
∴$P'(0,-16)$。综上所述,点$P'$的坐标为$(\frac {16}{5},0)$或(0,-16)。
查看更多完整答案,请扫码查看


