《2025年全优新同步八年级数学上册浙教版》

1.已知在Rt△ABC中,∠C= 90°,AC= 2,BC= 3,则AB的长为 ( )

A.4
B.5
C.$\sqrt{5}$
D.$\sqrt{13}$

答案： D

2.如图所示的阴影部分是一个长方形,则它的面积是 ( )
$A.14cm^2 B.10cm^2 C.48cm^2 D.20cm^2$
]

答案： D

3.已知一个直角三角形的两边长分别为6和10,则第三边的边长为 ( )

A.8
B.$2\sqrt{34}$
C.8或$2\sqrt{34}$
D.8或$\sqrt{34}$

答案： C

4.小明学了利用勾股定理在数轴上作一个无理数后,于是在如图所示的数轴上的2个单位长度的位置找一个点D,然后过点D作一条垂直于数轴的线段CD,CD为3个单位长度,以原点为圆心,以到点C的距离为半径作弧,交数轴于一点,则该点位置大致在数轴上 ( )

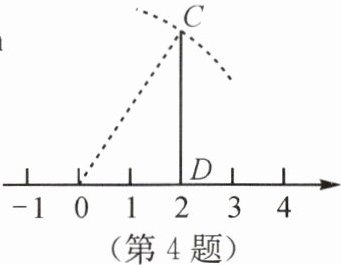
A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
]

答案： B【解析】由勾股定理得$OC=\sqrt {2^{2}+3^{2}}=\sqrt {13}$，
∵9＜13＜16，
∴$3＜\sqrt {13}＜4$。
∴该点位置大致在数轴上3和4之间。

5.如图所示,在Rt△ABC中,∠ACB= 90°,BC= 3,AC= 4。以AB为边在点C同侧作正方形ABDE,则阴影部分的面积为______。
]

答案： 19

6.如图所示,在△ABC中,∠C= 90°,D是BC边上一点,AB= 17cm,AD= 10cm,AC= 8cm,则BD的长为______。
]

答案： 9cm

7.如图所示,在△ABC中,AB= AC,BD⊥AC,BD= 6,E为AB边的中点,ED= 5,则DC= ______。
]

答案： 2

8.如图所示,在Rt△ABC中,∠C= 90°,a,b,c分别表示∠A,∠B,∠C的对边。
(1)已知c= 25,a:b= 4:3,求a,b。
(2)已知a= $\sqrt{6}$,∠A= 60°,求b,c。
]

答案：
(1)
∵在$Rt△ABC$中，$∠C=90^{\circ },c=25,a:b=4:3$，
∴设$a=4x$，则$b=3x$。
∵$c^{2}=a^{2}+b^{2}$，即$25^{2}=(4x)^{2}+(3x)^{2}$，解得$x=5$，
∴$a=4x=20,b=3x=15$。
(2)
∵$a=\sqrt {6},∠A=60^{\circ }$，
∴$c=2b$。
∴$(2b)^{2}=b^{2}+6$。
∴$b=\sqrt {2},c=2\sqrt {2}$。

9.如图所示,在△ABC中,∠ACB= 90°,AB= 5,BC= 4,CD⊥AB于点D。求：
(1)AC的长。
(2)△ABC的面积。
(3)CD的长。
]

答案：
(1)由勾股定理得$AC=\sqrt {AB^{2}-BC^{2}}=3$。
(2)$△ABC$的面积=$\frac {1}{2}×BC×AC=6$。
(3)$\frac {1}{2}×AB×CD=6$，解得$CD=\frac {12}{5}$。