《2025年全优新同步八年级数学上册浙教版》

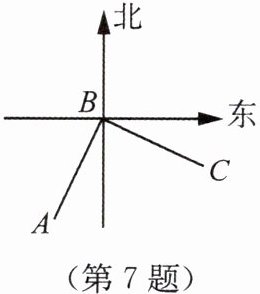
7. 如图所示,学校(记作A)在蕾蕾家(记作B)南偏西25°的方向上,且与蕾蕾家的距离是4km,若∠ABC= 90°,且AB= BC,则超市(记作C)在蕾蕾家的( )


A.南偏东65°的方向上,相距4km
B.南偏东55°的方向上,相距4km
C.北偏东55°的方向上,相距4km
D.北偏东65°的方向上,相距4km

答案： A

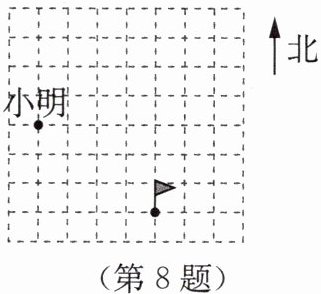
8. 小明、小华、小亮三人去看电影。如图所示为影院分布图,若分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系,他们这样描述自己的座位:①小明:表示我座位的坐标为(-2,3);②小华:在小明的座位向右走4个座位,再向上走2个座位,就可以找到我了;③小亮:小旗帜所在的位置就是我的座位了。小华、小亮座位的坐标分别为______。

答案： (2,5),(2,0)

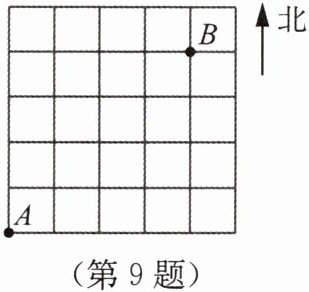
9. 常用的确定物体位置的方法有两种:一是通过建立平面直角坐标系,用坐标表示;二是通过方向和距离表示。如图所示,在5×5的边长为1的正方形组成的方格中,标有A,B两点(点A,B间的距离为n)。请你用两种不同的方法表述点B相对于点A的位置。

答案： 方法1:以点A为原点，水平方向为x轴，建立平面直角坐标系，则B(4,4)。
方法2:点B位于点A的东北方向(或北偏东45°等),距离点A$n$个单位长度处。

10. 在航空、航海等领域经常用距离和角度来确定点的位置。规定如下:在平面内取一个定点O,引一条射线Ox,对于平面内任何一点M,用ρ表示线段OM的长度,θ表示按逆时针方向从Ox转动到OM的度数,有序数对(ρ,θ)就叫做点M的极坐标,这样建立的坐标系叫做极坐标系。
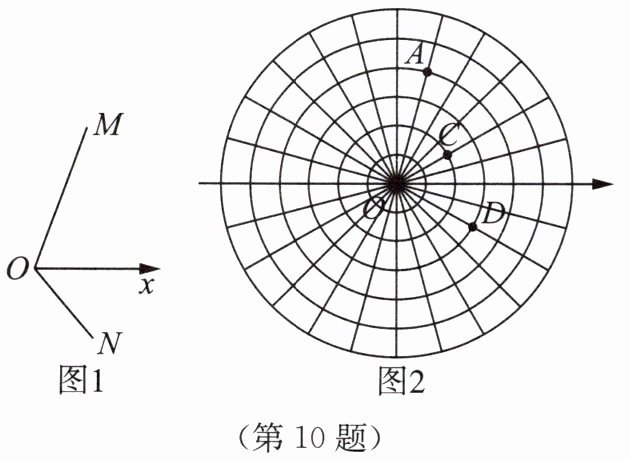
例如:如图1所示,MO的长为5个单位长度,OM与Ox的夹角为70°,则点M的极坐标为(5,70°);同理,NO的长为3个单位长度,ON与Ox的夹角为50°,则点N的极坐标为(3,-50°)。
如图2所示,已知过点O的所有射线等分圆周且相邻两射线的夹角为15°。
(1)点A的极坐标是______,点D的极坐标是______。
(2)请在图2中标出点B(5,45°),E(2,-90°)的位置。
(3)请你设计一条路线,能从点B运动到点C。

答案：

(1)(4,75°)　(3,-30°)
(2)如图所示。
　　　　　　　
(3)点B→(4,45°)→(3,45°)→(3,30°)→点C。(答案不唯一)