《2025年全优新同步八年级数学上册浙教版》

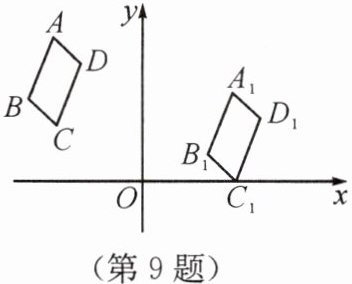
9. 如图所示,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移,得到四边形$A_1B_1C_1D_1,$已知点$A(-3,5),B(-4,3),A_1(3,3),$则点$B_1$的坐标为______。

答案： (2,1)

10. 在平面直角坐标系中,若点M(1-m,m+2)与点N(2m+3,m+2)之间的距离是5,则m= ______。

答案： $-\frac{7}{3}$或1

11. 在平面直角坐标系中,点M的坐标为(a,-2a)。
(1)当a= -1时,点M在第______象限。
(2)将点M先向左平移2个单位,再向上平移1个单位后得到点N,当点N在第三象限时,求a的取值范围。

答案：
(1)当$a=-1$时，点M的坐标为$(-1,2)$，
∴点M在第二象限。
(2)由题意得点N的坐标为$(a-2,-2a+1)$。
∵点N在第三象限，
∴$\left\{\begin{array}{l} a-2＜0,\\ -2a+1＜0,\end{array}\right. $解得$\frac{1}{2}＜a＜2$。
∴a的取值范围是$\frac{1}{2}＜a＜2$。

12. 如图所示,已知长方形ABCD四个顶点的坐标分别是A(2,-2√2),B(5,-2√2),C(5,-√2),D(2,-√2)。

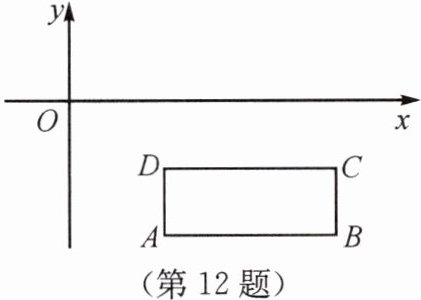
(1)求该长方形的面积。
(2)将长方形ABCD向上平移√2个单位长度,求所得的四边形A'B'C'D'的四个顶点的坐标。

答案：
(1)观察图形可知$AB=5-2=3$，$BC=-\sqrt{2}-(-2\sqrt{2})=\sqrt{2}$，
∴该长方形的面积是$3\sqrt{2}$。
(2)
∵将长方形ABCD向上平移$\sqrt{2}$个单位长度，
∴所得的四边形$A'B'C'D'$的四个顶点的坐标分别为:$A'(2,-\sqrt{2})$，$B'(5,-\sqrt{2})$，$C'(5,0)$，$D(2,0)$。

13. 如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1),…根据这个规律探索可得,第100个点的坐标 ( )


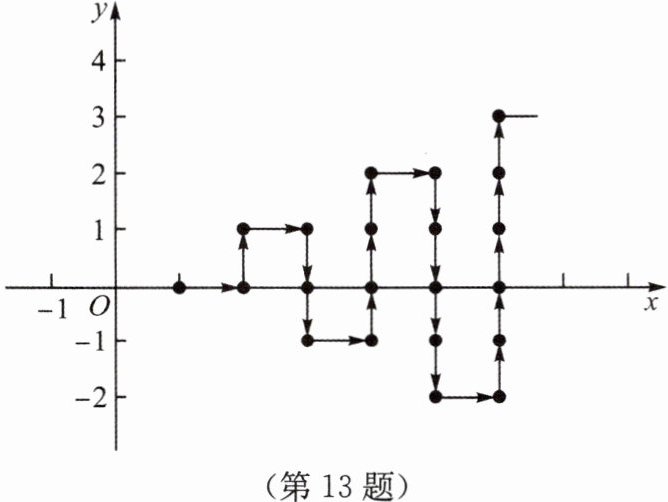
A.(14,0)
B.(14,-1)
C.(14,1)
D.(14,2)

答案： D 【解析】由图可知，横坐标是1的点共有1个，横坐标是2的点共有2个，横坐标是3的点共有3个，横坐标是4的点共有4个，……横坐标是n的点共有n个，$1+2+3+\cdots +n=\frac{n(n+1)}{2}$，当$n=13$时，$\frac{13× (13+1)}{2}=91$，当$n=14$时，$\frac{14× (14+1)}{2}=105$，
∴第100个点的横坐标是14。
∵$100-91=9$，
∴第100个点是横坐标为14的点中的第9个点。
∵其中第7个点的纵坐标是0，
∴第9个点的纵坐标是2。
∴第100个点的坐标是$(14,2)$。故选D。