《2025年全优新同步八年级数学上册浙教版》

1. 已知三角形的三边长均为偶数,其中两边长分别为2和8,则第三边长为______。

答案： 8

2. 如图所示,在△ABC中,∠A= 90°,点E,F分别在AB,AC边上,D是BC边上一动点(点D与点B,C不重合)。若∠1= 60°,则∠2+∠3= ______。

答案： 150°

3. 如图所示,在△ABC中,∠ABC= 60°,∠ACB= 80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数为( )

A.100°
B.110°
C.115°
D.120°

答案： B

4. 如图所示,D是BC的中点,E是AC的中点,若S△ADE= 2,则S△ABC= ______。

答案： 8

5. 如图所示,已知AC= DC,AB= DE,CB= CE。求证：∠1= ∠2。

答案： 设AC与DE交于点F。在△ABC和△DEC中，
∵{AC=DC，AB=DE，CB=CE}，
∴△ABC≌△DEC(SSS)。
∴∠A=∠D。
∵∠AFE=∠DFC，
∴∠1=∠2。

6. 如图所示,在△ABC中,∠C= 90°,D是AB边上的一点,DE⊥AB于点D,交AC于点M,且ED= AC,过点E作EF//BC分别交AB,AC于点F,N。
(1)求证：△ABC≌△EFD。
(2)若∠A= 25°,求∠EMN的度数。

答案：
(1)
∵DE⊥AB于点D，
∴∠EDF=90°。
∵∠C=90°，
∴∠C=∠EDF。
∵EF//BC，
∴∠B=∠EFD。在△ABC和△EFD中，
∵{∠C=∠EDF，∠B=∠EFD，AC=ED}，
∴△ABC≌△EFD(AAS)。
(2)
∵∠EDF=90°，
∴∠ADM=180° - ∠EDF=90°。在△ADM中，∠A+∠AMD+∠ADM=180°，且∠A=25°，
∴∠AMD=180° - ∠A - ∠ADM=65°。
∴∠EMN=∠AMD=65°。

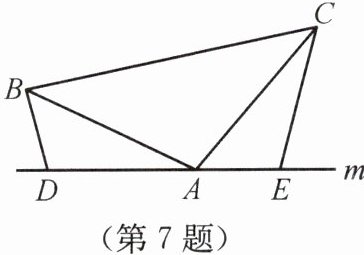
7. 如图所示,在△ABC中,AB= AC,D,A,E三点都在一条直线上,且∠BDA= ∠AEC= ∠BAC,BD= 3,CE= 6,则DE的长为______。

答案： 9【解析】
∵∠BDA=∠AEC=∠BAC，
∴∠DBA+∠BAD=∠BAD+∠CAE。
∴∠DBA=∠CAE。在△ADB和△CEA中，
∵{∠ABD=∠CAE，∠BDA=∠AEC，AB=CA}，
∴△ADB≌△CEA(AAS)。
∴BD=AE，AD=CE。
∴DE=AE+AD=BD+CE=3+6=9。

8. 如图所示,已知BD= BC,BE= CA,∠DBE= ∠C= 62°,∠BDE= 75°。
(1)求证：△ABC≌△EDB。
(2)试求∠AFD的度数。

答案：
(1)在△ABC和△EDB中，
∵{BC=DB，∠C=∠DBE，CA=BE}，
∴△ABC≌△EDB(SAS)。
(2)
∵∠BDE=75°，∠DBE=62°，
∴∠E=180° - ∠BDE - ∠DBE=43°。
∵△ABC≌△EDB，
∴∠A=∠E=43°。
∴∠AFD=∠BDE - ∠A=75° - 43°=32°。