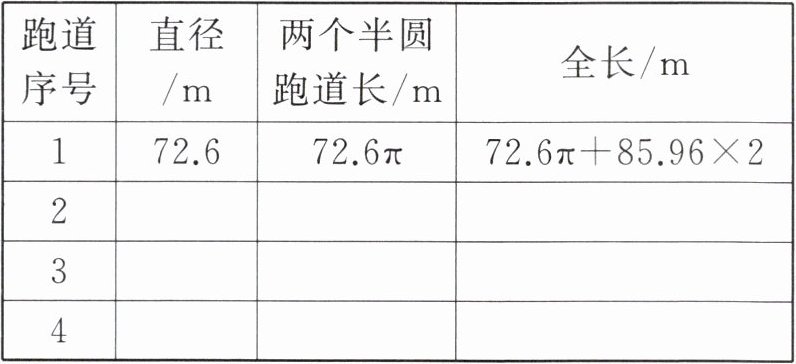
一、根据下右图中的数据计算并填写下表。(跑道长用含π的式子表示)
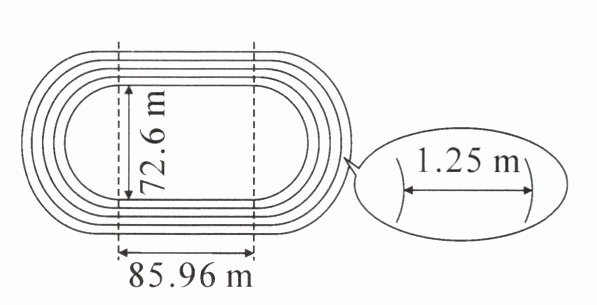
发现:如果以内侧跑道一圈为标准跑一圈,外圈跑道每一道的起跑线要比前一道提前(
| 跑道序号 | 直径/m | 两个半圆跑道长/m | 全长/m |
| :------- | :----- | :--------------- | :----- |
| 1 | 72.6 |
| 2 |
| 3 |
| 4 |


发现:如果以内侧跑道一圈为标准跑一圈,外圈跑道每一道的起跑线要比前一道提前(
7.85
)m。| 跑道序号 | 直径/m | 两个半圆跑道长/m | 全长/m |
| :------- | :----- | :--------------- | :----- |
| 1 | 72.6 |
72.6π
| 72.6π + 85.96× 2
|| 2 |
75.1
| 75.1π
| 75.1π + 85.96× 2
|| 3 |
77.6
| 77.6π
| 77.6π + 85.96× 2
|| 4 |
80.1
| 80.1π
| 80.1π + 85.96× 2
|
答案:
解析:本题主要考查圆的周长公式。
内圈跑道的直径确定后,外圈跑道的直径可以通过在内圈跑道直径的基础上依次增加$2× 1.25=2.5$($m$)来计算。
圆的周长公式为:$周长=\pi × 直径$。
跑道全长等于两个半圆跑道长加上两个直跑道长。
跑道$2$的直径为:
$72.6+2.5=75.1$($m$)。
两个半圆跑道长为:
$75.1\pi$($m$)。
全长为:
$(75.1\pi +85.96× 2)$ $m$。
跑道$3$的直径为:
$75.1+2.5=77.6$($m$)。
两个半圆跑道长为:
$77.6\pi$($m$)。
全长为:
$(77.6\pi +85.96× 2)$ $m$。
跑道$4$的直径为:
$77.6+2.5=80.1$($m$)。
两个半圆跑道长为:
$80.1\pi$($m$)。
全长为:
$(80.1\pi +85.96× 2)$ $m$。
每一道的起跑线要比前一道提前:
$2.5\pi\approx 2.5× 3.14=7.85$($m$)。
答案:
| 跑道序号 | 直径/m | 两个半圆跑道长/m | 全长/m |
| :------- | :----- | :--------------- | :----- |
| 1 | 72.6 | $72.6\pi$ | $72.6\pi + 85.96× 2$ |
| 2 | 75.1 | $75.1\pi$ | $75.1\pi + 85.96× 2$ |
| 3 | 77.6 | $77.6\pi$ | $77.6\pi + 85.96× 2$ |
| 4 | 80.1 | $80.1\pi$ | $80.1\pi + 85.96× 2$ |
$7.85$。
内圈跑道的直径确定后,外圈跑道的直径可以通过在内圈跑道直径的基础上依次增加$2× 1.25=2.5$($m$)来计算。
圆的周长公式为:$周长=\pi × 直径$。
跑道全长等于两个半圆跑道长加上两个直跑道长。
跑道$2$的直径为:
$72.6+2.5=75.1$($m$)。
两个半圆跑道长为:
$75.1\pi$($m$)。
全长为:
$(75.1\pi +85.96× 2)$ $m$。
跑道$3$的直径为:
$75.1+2.5=77.6$($m$)。
两个半圆跑道长为:
$77.6\pi$($m$)。
全长为:
$(77.6\pi +85.96× 2)$ $m$。
跑道$4$的直径为:
$77.6+2.5=80.1$($m$)。
两个半圆跑道长为:
$80.1\pi$($m$)。
全长为:
$(80.1\pi +85.96× 2)$ $m$。
每一道的起跑线要比前一道提前:
$2.5\pi\approx 2.5× 3.14=7.85$($m$)。
答案:
| 跑道序号 | 直径/m | 两个半圆跑道长/m | 全长/m |
| :------- | :----- | :--------------- | :----- |
| 1 | 72.6 | $72.6\pi$ | $72.6\pi + 85.96× 2$ |
| 2 | 75.1 | $75.1\pi$ | $75.1\pi + 85.96× 2$ |
| 3 | 77.6 | $77.6\pi$ | $77.6\pi + 85.96× 2$ |
| 4 | 80.1 | $80.1\pi$ | $80.1\pi + 85.96× 2$ |
$7.85$。
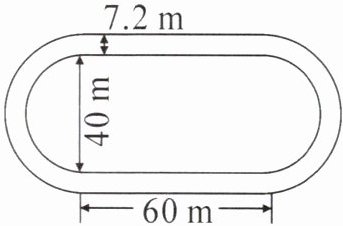
二、如图,一条跑道的宽是7.2 m,这条跑道最内侧和最外侧的周长差是多少米?

答案:
最内侧圆的直径为40m,半径为20m,周长为$2×3.14×20 = 125.6$m。
最外侧圆的半径为$20 + 7.2=27.2$m,周长为$2×3.14×27.2=170.816$m。
直道部分长度相同,周长差为$170.816 - 125.6 = 45.216$m。
答:这条跑道最内侧和最外侧的周长差是45.216米。
最外侧圆的半径为$20 + 7.2=27.2$m,周长为$2×3.14×27.2=170.816$m。
直道部分长度相同,周长差为$170.816 - 125.6 = 45.216$m。
答:这条跑道最内侧和最外侧的周长差是45.216米。
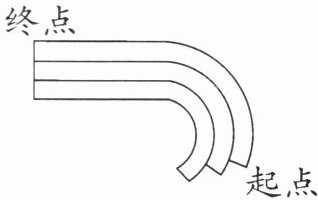
三、下右图是某学校200 m比赛赛程示意图,跑道宽1.25 m,相邻跑道中,外侧跑道运动员的起跑线应在内侧跑道运动员前面多少米?(得数保留两位小数)

答案:
200米比赛需跑一个弯道和一个直道,直道部分长度相同,差距在弯道部分。弯道为半圆,外侧跑道半径比内侧多1.25m。
外侧弯道周长 - 内侧弯道周长 = π×(r+1.25) - π×r = π×1.25 ≈ 3.14×1.25 = 3.925 ≈ 3.93(m)
答:外侧跑道运动员的起跑线应在内侧跑道运动员前面3.93米。
外侧弯道周长 - 内侧弯道周长 = π×(r+1.25) - π×r = π×1.25 ≈ 3.14×1.25 = 3.925 ≈ 3.93(m)
答:外侧跑道运动员的起跑线应在内侧跑道运动员前面3.93米。
四、【拓展题】下面右边是某校新建成的塑胶跑道,直跑道长85.96 m,第一条半圆形跑道内圈的直径为72.6 m,每条跑道宽1.2 m。
1. 小华沿最外圈这条跑道的外边线跑一圈,他跑了多少米?
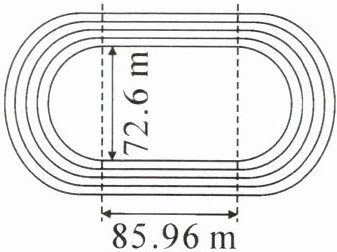
2. 如果进行400 m短跑比赛,那么第三条跑道的起跑线要比第一条跑道的起跑线提前多少米?
1. 小华沿最外圈这条跑道的外边线跑一圈,他跑了多少米?

2. 如果进行400 m短跑比赛,那么第三条跑道的起跑线要比第一条跑道的起跑线提前多少米?
答案:
1. 最外圈直径:72.6 + 1.2×2×跑道数量(假设跑道为4条,最外圈宽1.2×4=4.8m),直径=72.6 + 4.8×2=82.2m(注:根据常见跑道设计,通常为4-8条跑道,此处按最外圈计算,宽1.2×n,若图中为4条跑道,则直径=72.6+1.2×4×2=72.6+9.6=82.2m)。
周长=2×85.96 + 3.14×82.2=171.92 + 258.108=429.028m。
2. 第三条跑道比第一条跑道宽1.2×2=2.4m,直径差=2×2.4=4.8m,周长差=3.14×4.8=15.072m。
1. 429.028米
2. 15.072米
周长=2×85.96 + 3.14×82.2=171.92 + 258.108=429.028m。
2. 第三条跑道比第一条跑道宽1.2×2=2.4m,直径差=2×2.4=4.8m,周长差=3.14×4.8=15.072m。
1. 429.028米
2. 15.072米
查看更多完整答案,请扫码查看


