1. 小圆的直径和大圆的半径相等,小圆面积是大圆面积的(
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
D.$\frac{1}{8}$
B
)。A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
D.$\frac{1}{8}$
答案:
解析:本题主要考查圆的面积公式及计算。
设小圆的直径为$d$,则大圆的半径也为$d$,
小圆的半径为:$\frac{d}{2}$,
根据圆的面积公式:$S = \pi r^2$,其中$S$是面积,$r$是半径,
可得:
小圆的面积为:$\pi × (\frac{d}{2})^2 = \frac{\pi d^2}{4}$,
大圆的面积为:$\pi d^2$,
小圆面积与大圆面积的比值为:
$\frac{\frac{\pi d^2}{4}}{\pi d^2} = \frac{1}{4}$,
所以,小圆面积是大圆面积的$\frac{1}{4}$。
答案:B.$\frac{1}{4}$。
设小圆的直径为$d$,则大圆的半径也为$d$,
小圆的半径为:$\frac{d}{2}$,
根据圆的面积公式:$S = \pi r^2$,其中$S$是面积,$r$是半径,
可得:
小圆的面积为:$\pi × (\frac{d}{2})^2 = \frac{\pi d^2}{4}$,
大圆的面积为:$\pi d^2$,
小圆面积与大圆面积的比值为:
$\frac{\frac{\pi d^2}{4}}{\pi d^2} = \frac{1}{4}$,
所以,小圆面积是大圆面积的$\frac{1}{4}$。
答案:B.$\frac{1}{4}$。
2. 一个圆环,内圆半径是4 cm,外圆半径是5 cm,计算这个圆环面积,下面列式正确的是(
A.$3.14×5^{2}-4^{2}$
B.$3.14×(5-4)^{2}$
C.$3.14×5^{2}-3.14×4^{2}$
D.以上均正确
C
)。A.$3.14×5^{2}-4^{2}$
B.$3.14×(5-4)^{2}$
C.$3.14×5^{2}-3.14×4^{2}$
D.以上均正确
答案:
解析:本题考查圆环面积的计算方法。圆环的面积等于外圆的面积减去内圆的面积。圆的面积公式为$S = \pi r^{2}$,其中$r$为圆的半径。外圆半径是$5 cm$,则外圆面积为$3.14×5^{2}$;内圆半径是$4 cm$,则内圆面积为$3.14×4^{2}$,所以圆环面积为$3.14×5^{2}-3.14×4^{2}$。
答案:C
答案:C
二、求下面各图中阴影部分的周长和面积。(单位:cm)
1.
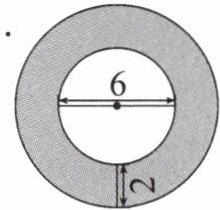
2.
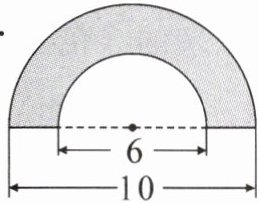
1.

2.

答案:
1. 分析题1:
考查知识点:本题主要考查圆环的周长和面积计算。
解题方法:
周长计算:阴影部分的周长是大圆周长与小圆周长之和。根据圆的周长公式$C = \pi d$($C$表示周长,$d$表示直径),分别计算大圆和小圆的周长,再将它们相加。
面积计算:阴影部分的面积是大圆面积与小圆面积之差。根据圆的面积公式$S=\pi r^{2}$($S$表示面积,$r$表示半径),分别计算大圆和小圆的面积,再将它们相减。
计算过程:
周长:
大圆直径$D = 6 + 2×2=10$($cm$),大圆周长$C_{大}=\pi D = 3.14×10 = 31.4$($cm$)。
小圆直径$d = 6$($cm$),小圆周长$C_{小}=\pi d=3.14×6 = 18.84$($cm$)。
阴影部分周长$C = C_{大}+C_{小}=31.4 + 18.84=50.24$($cm$)。
面积:
大圆半径$R=\frac{6 + 2×2}{2}=5$($cm$),大圆面积$S_{大}=\pi R^{2}=3.14×5^{2}=3.14×25 = 78.5$($cm^{2}$)。
小圆半径$r=\frac{6}{2}=3$($cm$),小圆面积$S_{小}=\pi r^{2}=3.14×3^{2}=3.14×9 = 28.26$($cm^{2}$)。
阴影部分面积$S = S_{大}-S_{小}=78.5-28.26 = 50.24$($cm^{2}$)。
答案:
周长:$50.24$ $cm$。
面积:$50.24$ $cm^{2}$。
2. 分析题2:
考查知识点:本题主要考查圆环面积以及半圆周长的组合计算。
解题方法:
周长计算:阴影部分的周长是大半圆的弧长、小半圆的弧长以及大半圆直径与小半圆直径之差的和。根据圆的弧长公式$l=\pi r$($l$表示弧长,$r$表示半径),分别计算大半圆和小半圆的弧长,再加上大半圆直径与小半圆直径之差。
面积计算:阴影部分的面积是大半圆面积与小半圆面积之差。根据圆的面积公式$S = \pi r^{2}$,分别计算大半圆和小半圆的面积,再将它们相减。
计算过程:
周长:
大半圆直径$D = 10$($cm$),大半圆半径$R=\frac{10}{2}=5$($cm$),大半圆弧长$l_{大}=\frac{1}{2}×\pi D=\frac{1}{2}×3.14×10 = 15.7$($cm$)。
小半圆直径$d = 6$($cm$),小半圆半径$r=\frac{6}{2}=3$($cm$),小半圆弧长$l_{小}=\frac{1}{2}×\pi d=\frac{1}{2}×3.14×6 = 9.42$($cm$)。
大半圆直径与小半圆直径之差为$10 - 6 = 4$($cm$)。
阴影部分周长$C=l_{大}+l_{小}+4=15.7 + 9.42+4=29.12$($cm$)。
面积:
大半圆面积$S_{大}=\frac{1}{2}×\pi R^{2}=\frac{1}{2}×3.14×5^{2}=\frac{1}{2}×3.14×25 = 39.25$($cm^{2}$)。
小半圆面积$S_{小}=\frac{1}{2}×\pi r^{2}=\frac{1}{2}×3.14×3^{2}=\frac{1}{2}×3.14×9 = 14.13$($cm^{2}$)。
阴影部分面积$S = S_{大}-S_{小}=39.25-14.13 = 25.12$($cm^{2}$)。
答案:
周长:$29.12$ $cm$。
面积:$25.12$ $cm^{2}$。
考查知识点:本题主要考查圆环的周长和面积计算。
解题方法:
周长计算:阴影部分的周长是大圆周长与小圆周长之和。根据圆的周长公式$C = \pi d$($C$表示周长,$d$表示直径),分别计算大圆和小圆的周长,再将它们相加。
面积计算:阴影部分的面积是大圆面积与小圆面积之差。根据圆的面积公式$S=\pi r^{2}$($S$表示面积,$r$表示半径),分别计算大圆和小圆的面积,再将它们相减。
计算过程:
周长:
大圆直径$D = 6 + 2×2=10$($cm$),大圆周长$C_{大}=\pi D = 3.14×10 = 31.4$($cm$)。
小圆直径$d = 6$($cm$),小圆周长$C_{小}=\pi d=3.14×6 = 18.84$($cm$)。
阴影部分周长$C = C_{大}+C_{小}=31.4 + 18.84=50.24$($cm$)。
面积:
大圆半径$R=\frac{6 + 2×2}{2}=5$($cm$),大圆面积$S_{大}=\pi R^{2}=3.14×5^{2}=3.14×25 = 78.5$($cm^{2}$)。
小圆半径$r=\frac{6}{2}=3$($cm$),小圆面积$S_{小}=\pi r^{2}=3.14×3^{2}=3.14×9 = 28.26$($cm^{2}$)。
阴影部分面积$S = S_{大}-S_{小}=78.5-28.26 = 50.24$($cm^{2}$)。
答案:
周长:$50.24$ $cm$。
面积:$50.24$ $cm^{2}$。
2. 分析题2:
考查知识点:本题主要考查圆环面积以及半圆周长的组合计算。
解题方法:
周长计算:阴影部分的周长是大半圆的弧长、小半圆的弧长以及大半圆直径与小半圆直径之差的和。根据圆的弧长公式$l=\pi r$($l$表示弧长,$r$表示半径),分别计算大半圆和小半圆的弧长,再加上大半圆直径与小半圆直径之差。
面积计算:阴影部分的面积是大半圆面积与小半圆面积之差。根据圆的面积公式$S = \pi r^{2}$,分别计算大半圆和小半圆的面积,再将它们相减。
计算过程:
周长:
大半圆直径$D = 10$($cm$),大半圆半径$R=\frac{10}{2}=5$($cm$),大半圆弧长$l_{大}=\frac{1}{2}×\pi D=\frac{1}{2}×3.14×10 = 15.7$($cm$)。
小半圆直径$d = 6$($cm$),小半圆半径$r=\frac{6}{2}=3$($cm$),小半圆弧长$l_{小}=\frac{1}{2}×\pi d=\frac{1}{2}×3.14×6 = 9.42$($cm$)。
大半圆直径与小半圆直径之差为$10 - 6 = 4$($cm$)。
阴影部分周长$C=l_{大}+l_{小}+4=15.7 + 9.42+4=29.12$($cm$)。
面积:
大半圆面积$S_{大}=\frac{1}{2}×\pi R^{2}=\frac{1}{2}×3.14×5^{2}=\frac{1}{2}×3.14×25 = 39.25$($cm^{2}$)。
小半圆面积$S_{小}=\frac{1}{2}×\pi r^{2}=\frac{1}{2}×3.14×3^{2}=\frac{1}{2}×3.14×9 = 14.13$($cm^{2}$)。
阴影部分面积$S = S_{大}-S_{小}=39.25-14.13 = 25.12$($cm^{2}$)。
答案:
周长:$29.12$ $cm$。
面积:$25.12$ $cm^{2}$。
三、学校草地上原来有一个射程是20米的自动旋转洒水器,新学期更换了新的自动旋转洒水器,射程达到25米。喷洒面积增加了多少平方米?
答案:
解析:本题考查圆环的面积计算。需要用到圆环面积的计算公式,即大圆面积减去小圆面积。
原来的洒水器射程为20米,即原来圆的半径$r_1$是20米;
新的洒水器射程为25米,即新的圆的半径$r_2$是25米。
圆的面积公式为:$S = \pi r^2$。
所以,原来圆的面积$S_1 = \pi × (20)^2=400\pi$,
新的圆的面积$S_2 = \pi × (25)^2=625\pi$。
喷洒面积的增加量 = 新的圆的面积 - 原来圆的面积
$= 625\pi - 400\pi$
$= 225\pi$
$\pi$取3.14,得到:
喷洒面积的增加量 $\approx 225 × 3.14 = 706.5$(平方米)。
答案:喷洒面积增加了706.5平方米。
原来的洒水器射程为20米,即原来圆的半径$r_1$是20米;
新的洒水器射程为25米,即新的圆的半径$r_2$是25米。
圆的面积公式为:$S = \pi r^2$。
所以,原来圆的面积$S_1 = \pi × (20)^2=400\pi$,
新的圆的面积$S_2 = \pi × (25)^2=625\pi$。
喷洒面积的增加量 = 新的圆的面积 - 原来圆的面积
$= 625\pi - 400\pi$
$= 225\pi$
$\pi$取3.14,得到:
喷洒面积的增加量 $\approx 225 × 3.14 = 706.5$(平方米)。
答案:喷洒面积增加了706.5平方米。
四、如图,阴影部分的面积是$40 cm^2,$圆环的面积是多少平方厘米?
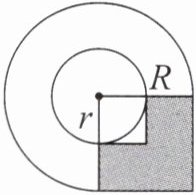

答案:
设大圆半径为$R$,小圆半径为$r$。
阴影部分面积为大正方形面积减去小正方形面积,即$R^2 - r^2 = 40\,cm^2$。
圆环面积公式为$\pi(R^2 - r^2)$,代入得:
$3.14×40 = 125.6\,cm^2$。
答:圆环的面积是$125.6$平方厘米。
阴影部分面积为大正方形面积减去小正方形面积,即$R^2 - r^2 = 40\,cm^2$。
圆环面积公式为$\pi(R^2 - r^2)$,代入得:
$3.14×40 = 125.6\,cm^2$。
答:圆环的面积是$125.6$平方厘米。
五、【拓展题】如图,三个同心圆的半径之比是1:3:5,阴影部分与空白部分的面积比是多少?
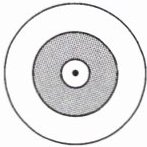

答案:
设三个同心圆的半径分别为$r=1$、$3r=3$、$5r=5$。
阴影部分面积:$\pi×3^2 - \pi×1^2 = 9\pi - \pi = 8\pi$
空白部分面积:$\pi×5^2 - 8\pi = 25\pi - 8\pi = 17\pi$
阴影部分与空白部分的面积比:$8\pi:17\pi = 8:17$
答:阴影部分与空白部分的面积比是$8:17$。
阴影部分面积:$\pi×3^2 - \pi×1^2 = 9\pi - \pi = 8\pi$
空白部分面积:$\pi×5^2 - 8\pi = 25\pi - 8\pi = 17\pi$
阴影部分与空白部分的面积比:$8\pi:17\pi = 8:17$
答:阴影部分与空白部分的面积比是$8:17$。
查看更多完整答案,请扫码查看


