《2025年配套综合练习甘肃九年级物理全一册人教版》

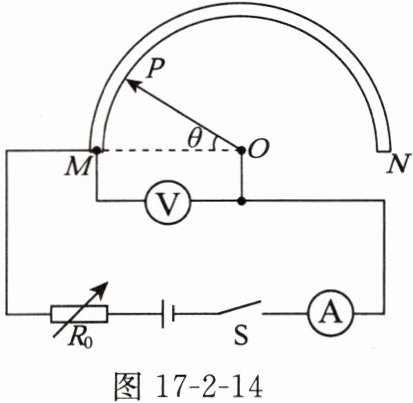
18. 新房装修时,工人经常用普通量角器测量一些角度,不方便读数。小明根据所学的知识设计了电子量角器,电路如图 17-2-14 所示,电流表的测量范围为 $ 0\sim0.6 A $,电压表的测量范围为 $ 0\sim3 V $,$ O $ 为半圆弧电阻 $ MN $ 的圆心,金属滑片 $ OP $ 为半径,与半圆弧接触良好,接入电路的电阻 $ R_{MP} $ 与指针旋转角度 $ \theta $ 成正比,电源电压恒为 $ 6 V $,$ R_0 $ 为电阻箱。将滑片 $ OP $ 旋转至 $ M $ 处,闭合开关,调节 $ R_0 $ 的阻值,使电路中电流为 $ 0.6 A $。
(1)求电阻箱接入电路的阻值。
(2)保持 $ R_0 $ 接入电路的阻值不变,调节 $ \theta $ 为 $ 90^{\circ} $ 时,电流表示数为 $ 0.3 A $,求此时电压表示数。
(3)为能满足测量 $ 0\sim180^{\circ} $ 的要求,重新调节电阻箱 $ R_0 $,求满足要求的 $ R_0 $ 的最小阻值。

答案： 1. （1）
解：当滑片$OP$旋转至$M$处时，$R_{MP}=0$，此时电路中只有$R_0$接入电路。
根据欧姆定律$I = \frac{U}{R}$，可得$R_0=\frac{U}{I}$，已知$U = 6V$，$I = 0.6A$。
则$R_0=\frac{6V}{0.6A}=10\Omega$。
2. （2）
解：保持$R_0$接入电路的阻值不变，$R_0 = 10\Omega$，电流$I'=0.3A$。
根据$U_0 = I'R_0$，可得$U_0=0.3A×10\Omega = 3V$。
因为电源电压$U = 6V$，根据串联电路电压特点$U = U_0+U_V$。
所以电压表示数$U_V=U - U_0=6V - 3V = 3V$。
3. （3）
解：设$R_{MP}=k\theta$（$k$为比例常数）。
当$\theta = 90^{\circ}$时，$I' = 0.3A$，$U_V = 3V$，则$R_{MP}=\frac{U_V}{I'}=\frac{3V}{0.3A}=10\Omega$，所以$k=\frac{10\Omega}{90^{\circ}}=\frac{1}{9}\Omega/^{\circ}$。
当$\theta = 180^{\circ}$时，$R_{MP最大}=k×180^{\circ}=\frac{1}{9}\Omega/^{\circ}×180^{\circ}=20\Omega$。
为了保证电压表不超过量程（$U_V\leq3V$），当$U_V = 3V$，$R_{MP最大}=20\Omega$时，此时电路中的电流$I_{min}=\frac{U_V}{R_{MP最大}}=\frac{3V}{20\Omega}=0.15A$。
根据串联电路电压特点$U_0'=U - U_V=6V - 3V = 3V$。
再根据欧姆定律$R_0=\frac{U_0'}{I_{min}}$，可得$R_0=\frac{3V}{0.15A}=20\Omega$。
综上，（1）电阻箱接入电路的阻值为$10\Omega$；（2）此时电压表示数为$3V$；（3）满足要求的$R_0$的最小阻值为$20\Omega$。