第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
9. 如图,四边形 $ABCD$ 和 $CEFG$ 都是矩形,若 $AB = a$,$AD = b$,则阴影部分的面积是
多少?
多少?

答案:
$9. \frac{1}{2}ab$
10. 甲、乙两家超市以相同的价格出售同样的商品,各自推出不同的优惠方案:在甲超市
累计购买商品超过 $400$ 元后,超过部分按原价的 $7$ 折优惠;在乙超市购买商品全部按原价的 $8$
折优惠.
(1)若顾客累计需购买商品的价格为 $280$ 元,则在两家超市购买所付的费用各为多少元?
(2)若顾客累计需购买商品的价格为 $1100$ 元,则在两家超市购买所付的费用各为多少元?
(3)设顾客累计需购买商品的价格为 $x$ 元,用含 $x$ 的代数式分别表示在两家超市购买所
付的费用.
累计购买商品超过 $400$ 元后,超过部分按原价的 $7$ 折优惠;在乙超市购买商品全部按原价的 $8$
折优惠.
(1)若顾客累计需购买商品的价格为 $280$ 元,则在两家超市购买所付的费用各为多少元?
(2)若顾客累计需购买商品的价格为 $1100$ 元,则在两家超市购买所付的费用各为多少元?
(3)设顾客累计需购买商品的价格为 $x$ 元,用含 $x$ 的代数式分别表示在两家超市购买所
付的费用.
答案:
10.
(1) 在甲超市购买所付的费用是280元,在乙超市购买所付的费用是280×80\% = 224(元)
(2) 在甲超市购买所付的费用是400+(1100-400)×70\% = 890(元),在乙超市购买所付的费用是1100×80\% = 880(元)
(3) 在甲超市购买不超过400元时所付的费用为x元,超过400元时所付的费用为(0.7x+120)元,在乙超市购买所付的费用为0.8x元
(1) 在甲超市购买所付的费用是280元,在乙超市购买所付的费用是280×80\% = 224(元)
(2) 在甲超市购买所付的费用是400+(1100-400)×70\% = 890(元),在乙超市购买所付的费用是1100×80\% = 880(元)
(3) 在甲超市购买不超过400元时所付的费用为x元,超过400元时所付的费用为(0.7x+120)元,在乙超市购买所付的费用为0.8x元
11. 已知:$1 + 2 = \frac{2×(1 + 2)}{2} = 3$;$1 + 2 + 3 = \frac{3×(1 + 3)}{2} = 6$;$1 + 2 + 3 + 4 = \frac{4×(1 + 4)}{2} = 10$.
由此计算:
(1)$1 + 2 + 3 + 4 + ·s + 100$;
(2)$1 + 2 + 3 + 4 + ·s + n$.
由此计算:
(1)$1 + 2 + 3 + 4 + ·s + 100$;
(2)$1 + 2 + 3 + 4 + ·s + n$.
答案:
11.
(1) 原式$ = \frac{100×(1+100)}{2}=5050 (2) 1+2+3+⋯+n=\frac{n(1+n)}{2}$
(1) 原式$ = \frac{100×(1+100)}{2}=5050 (2) 1+2+3+⋯+n=\frac{n(1+n)}{2}$
12. 如图所示,在由火柴棒拼出的图形中,第 $n$ 个图形由 $n$ 个正六边形组成,通过观察可以发现:
(1)第 $4$ 个图形中火柴棒有
(2)前 $10$ 个图形中的火柴棒共有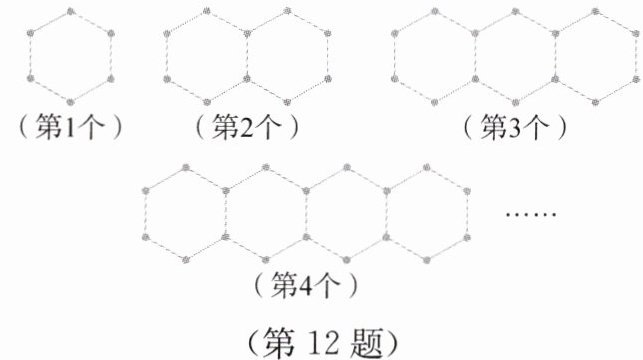
(1)第 $4$ 个图形中火柴棒有
21
根,第 $n$ 个图形中火柴棒有(5n+1)
根.(2)前 $10$ 个图形中的火柴棒共有
285
根.
答案:
12.
(1) 21 (5n+1)
(2) 285(提示:用倒序叠加法,可得共有$\frac{(6+51)×10}{2}=285$根)
(1) 21 (5n+1)
(2) 285(提示:用倒序叠加法,可得共有$\frac{(6+51)×10}{2}=285$根)
查看更多完整答案,请扫码查看


