《2025年学习检测七年级数学上册华师大版》

11. 用同样大小的黑、白两种颜色的棋子摆放成如图所示的正方形图案.

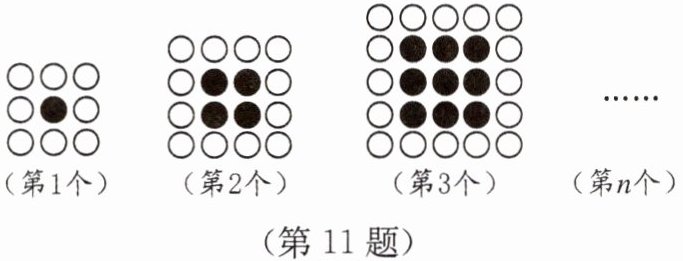
(第1个) (第2个) (第3个) (第$n$个)
第$n$个图案需要用黑色棋子多少枚?(用含有$n$的式子表示)

答案： 11. $n^2$

12. 看式子找规律，写数字：
$1 × 2$，$2 × 3$，$3 × 4$，$·s$.
(1) 总结出规律，并写出第10个、第30个和第48个数；
(2) 420是不是这一列数中的数? 如果是，是第几个数?

答案： 12.
(1) 规律：第$n$个数为$n(n + 1)$；110、930、2352
(2) 是，第20个