《2025年名校课堂七年级数学3上册人教版广东专版》

3. 【例2】(人教7上P51例1变式)计算：
(1)$3^4=$81；(2)$(-3)^4=$81；
(3)$4^3=$64；(4)$(-4)^3=$-64；
(5)$0.3^2=$0.09；(6)$(-0.3)^2=$0.09；
(7)$(\frac{2}{3})^3=$$\frac{8}{27}$；(8)$(-\frac{2}{3})^3=$$-\frac{8}{27}$.

答案： 3.
(1)81
(2)81
(3)64
(4)-64
(5)0.09
(6)0.09
(7)$\frac{8}{27}$
(8)$-\frac{8}{27}$

4. 计算：
(1)$(-1)^{10}=$1；(2)$(-10)^4=$10 000；
(3)$8^3=$512；(4)$0.1^3=$0.001；
(5)$0^3=$0；(6)$0^{2026}=$0；
(7)$(-\frac{1}{2})^3=$$-\frac{1}{8}$；(8)$0.2^2=$0.04.

答案： 4.
(1)1
(2)10 000
(3)512
(4)0.001
(5)0
(6)0
(7)$-\frac{1}{8}$
(8)0.04

5. 【例3】计算：
(1)$-3^2=$-9；
(2)$-(-3)^2=$-9；
(3)$-(-3)^3=$27；
(4)$\frac{-3^2}{2}=$$-\frac{9}{2}$.

答案： 5.
(1)-9
(2)-9
(3)27
(4)$-\frac{9}{2}$

6. 计算：
(1)$-1^{2026}=$-1；
(2)$-(-1)^{2025}=$1；
(3)$-(-0.4)^2=$-0.16；
(4)$\frac{-3}{(-2)^3}=$$\frac{3}{8}$.

答案： 6.
(1)-1
(2)1
(3)-0.16
(4)$\frac{3}{8}$

7. $(-3)^4$表示的意义是 （ ）

A.$-3×(-3)×(-3)×(-3)$
B.$-3+(-3)+(-3)+(-3)$
C.$-3×4$
D.$-3+4$

答案： 7.A

8. (1)在$(-\frac{1}{2})^5$中，底数是____，指数是____；
(2)在$(-10)^6$中，$-10$叫作，6叫作.$(-10)^6$是数(填“正”或“负”).

答案： 8.
(1)-7 8
(2)底数 指数 正

9. 计算：
(1)$(-4)^2=$16；
(2)$-4^2=$-16；
(3)$(-10)^4=$10 000；
(4)$(-10)^5=$-100 000；
(5)$-0.1^3=$-0.001；
(6)$-1^{99}=$-1；
(7)$-(-1)^{99}=$1；
(8)$-\frac{2^4}{3}=$$-\frac{16}{3}$.

答案： 9.
(1)16
(2)-16
(3)10 000
(4)-100 000
(5)-0.001
(6)-1
(7)1
(8)$-\frac{16}{3}$

10. 下列各组式子中，运算结果相同的是 (A)

A.$-2^3$和$(-2)^3$
B.$-(-2)^2$和$2^2$
C.$(-2)^2$和$-2^2$
D.$|-2^2|$和$-|-2^2|$

答案： 10.A

11. 计算：$\frac{\overbrace{2×2×2×…×2}^{m个2}}{\underbrace{3+3+3+…+3}_{n个3}}=$ （ ）

A.$\frac{2m}{3^n}$
B.$\frac{2^m}{3n}$
C.$\frac{2m}{n^3}$
D.$\frac{m^2}{3n}$

答案： 11.B

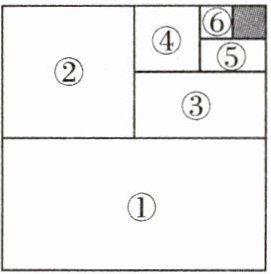
12. 北师大附属实验校本经典题 如图，将一张边长为1的正方形纸片分割成7个部分，部分①的面积是边长为1的正方形纸片面积的一半，部分②的面积是部分①面积的一半，部分③的面积是部分②面积的一半，依次类推.
(1)阴影部分的面积是多少？
(2)受(1)的启发，试求出$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^6}$的值.

答案： 12.解:
(1)阴影部分的面积是$\frac{1}{2^6}=\frac{1}{64}$.
(2)原式$=1-\frac{1}{2^6}=1-\frac{1}{64}=\frac{63}{64}$.