《2025年名校课堂七年级数学3上册人教版广东专版》

1. 某超市销售甲、乙两种商品，两种商品的相关信息如下表：

(1) 以上表格中 $ m $，$ n $ 的值分别为75，50%；
(2) 若该超市购进甲种商品的数量比乙种商品数量的 2 倍少 10 件，且在正常销售情况下售完这两种商品共获利 3050 元，求购进甲、乙两种商品各多少件.

答案： 1.解:
(1)75 50%
(2)设购进乙种商品x件,则购进甲种商品(2x-10)件.根据题意,得(60-40)(2x-10)+(75-50)x=3 050,解得x=50.则2x-10=2×50-10=90.
答:该超市购进甲种商品90件、乙种商品50件.

2. 新考向 数学文化 唐代大诗人李白喜好饮酒作诗，民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云：今携一壶酒，游春郊外走.逢朋加一倍，入店饮半斗.相逢三处店，饮尽壶中酒.试问能算士，如何知原有（注：古代一斗是 10 升）.大意是：李白在郊外春游时，做出这样一条约定，遇见朋友，到酒店里先将壶里的酒增加一倍，再喝掉其中的 5 升酒. 按照这样的约定，在第 3 个店里正好喝光了壶中的酒. 请问各位，壶中原有多少升酒？

答案： 2.解:设壶中原有x升酒.根据题意,得2[2(2x-5)-5]-5=0,解得x=35/8.
答:壶中原有35/8升酒.

3. A|兰生复旦校本经典题 王大伯两年前把一笔钱存入银行，定期 2 年，年利率为 2.25%，到期后得到本息和为 104500 元（不计复利）. 则王大伯当时存入银行多少钱？

答案： 3.解:设王大伯当时存入银行x元,则2年的利息为2×2.25%·x元.根据题意,得x+2×2.25%·x=104 500,解得x=100 000.
答:王大伯当时存入银行100 000元.

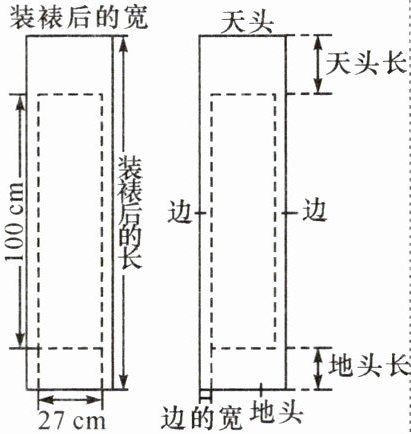
4. (2023·北京)对联是中华传统文化的瑰宝，对联装裱后，如图所示，上、下空白处分别称为天头和地头，左、右空白处统称为边. 一般情况下，天头长与地头长的比是 6:4，左、右边的宽相等，均为天头长与地头长之和的 $\frac{1}{10}$. 某人要装裱一副对联，对联的长为 100 cm，宽为 27 cm. 若要求装裱后的长是装裱后的宽的 4 倍，求边的宽和天头长.

答案： 4.解:设天头长为6x cm,地头长为4x cm,则左、右边的宽为x cm.根据题意,得100+(6x+4x)=4×(27+2x),解得x=4.
∴6x=24.
答:边的宽为4 cm,天头长为24 cm.